北京市石景山区高一下学期期末考试数学试卷
如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆内的黄豆数为225颗,以此实验数据为依据可以估计出椭圆的面积约为( ).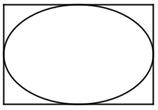
| A.16 | B.17 | C.18 | D.19 |
下面关于算法的说法正确的是( )
| A.秦九韶算法是求两个数的最大公约数的方法 |
| B.更相减损术是求多项式的值的方法 |
C.割圆术是采用正多边形面积逐渐逼近圆面积的算法计算圆周率 |
| D.以上结论皆错 |
已知△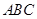 的三个内角满足
的三个内角满足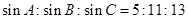 ,则△
,则△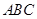 是( )
是( )
| A.等腰三角形 | B.锐角三角形 |
| C.直角三角形 | D.钝角三角形 |
某产品的广告费用 (万元)与销售额
(万元)与销售额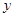 (万元)的统计数据如表,根据右表可得回归方程
(万元)的统计数据如表,根据右表可得回归方程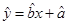 中的
中的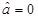 ,据此模型预报广告费用为6万元时销售额为( )
,据此模型预报广告费用为6万元时销售额为( )
 |
4 |
2 |
3 |
5 |
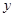 |
38 |
20 |
31 |
51 |
A.50 B.60 C.63 D.59
执行如图所示的程序框图,若“否”箭头分别指向①和②,则输出的结果分别是( )
A. |
B. |
C. |
D. |
某高中为了解在校高中生对参加某项社会实践活动的意向,拟采用分层抽样的方法从该校三个年级的高中生中抽取一个容量为300的样本进行调查.已知该校高一、高二、高三的人数之比为4∶5∶6,则应从高一年级抽取________名学生.
将数列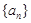 按如图所示的规律排成一个三角形表,并同时满足以下两个条件:
按如图所示的规律排成一个三角形表,并同时满足以下两个条件:
①各行的第一个数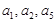 构成公差为
构成公差为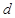 的等差数列;
的等差数列;
②从第二行起,每行各数按从左到右的顺序构成公比为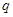 的等比数列.
的等比数列.
若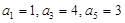 ,则
,则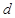 =_____________;
=_____________;
第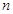 行的和
行的和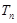 =__________________________.
=__________________________.
某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,整理得到数据分组及频率分布表和频率分布直方图:
| 分组 (日销售量) |
频率 (甲种酸奶) |
| [ 0,10] |
0.10 |
| (10,20] |
0.20 |
| (20,30] |
0.30 |
| (30,40] |
0.25 |
| (40,50] |
0.15 |

(Ⅰ)写出频率分布直方图中的 的值,并作出甲种酸奶日销售量的频率分布直方图;
的值,并作出甲种酸奶日销售量的频率分布直方图;
答: =________________;
=________________;
(Ⅱ)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为 ,
, ,试比较
,试比较 与
与 的大小.(只需写出结论).
的大小.(只需写出结论).
答: ______________
______________
某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过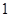 小时收费
小时收费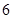 元,超过
元,超过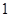 小时的部分每小时收费
小时的部分每小时收费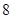 元(不足
元(不足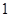 小时的部分按
小时的部分按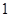 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过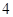 小时.
小时.
(Ⅰ)设甲停车付费a元.依据题意,填写下表:
| 甲停车时长 (小时) |
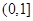 |
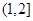 |
 |
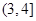 |
| 甲停车费a (元) |
|
|
|
|
(Ⅱ)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为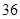 元的概率;
元的概率;
(Ⅲ)若甲停车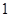 小时以上且不超过
小时以上且不超过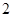 小时的概率为
小时的概率为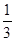 ,停车付费多于
,停车付费多于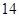 元的概率为
元的概率为 ,求甲停车付费恰为
,求甲停车付费恰为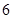 元的概率.
元的概率.
某机床厂2011年年初用98万元购进一台数控机床,并立即投入生产使用.计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元;该机床使用后,每年的总收入为50万元.
设使用 年后数控机床的盈利额为
年后数控机床的盈利额为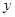 万元.
万元.
(Ⅰ)写出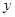 与
与 之间的函数关系式;
之间的函数关系式;
(Ⅱ)使用若干年后,对机床的处理方案有两种:
方案一:当年平均盈利额达到最大值时,以 万元价格处理该机床;
万元价格处理该机床;
方案二:当盈利额达到最大值时,以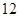 万元价格处理该机床;
万元价格处理该机床;
请你研究一下哪种方案处理较为合理?并说明理由.
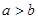 ,则
,则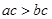
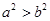
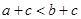 ,
,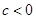 ,则
,则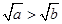 ,则
,则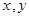 满足约束条件
满足约束条件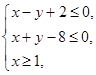 ,则
,则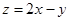 的最大值为( )
的最大值为( )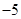
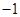
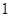
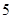
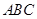 的内角
的内角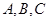 所对的边为
所对的边为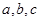 ,
,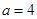 ,
,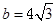 ,
, ,则
,则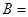 ( )
( )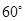
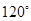
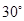
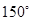
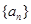 中,若
中,若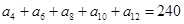 ,则
,则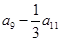 的值为( )
的值为( )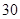
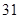

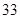
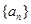 是公比为
是公比为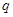 的等比数列,
的等比数列,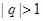 ,令
,令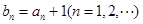 ,若数列
,若数列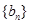 有连续四项在集合
有连续四项在集合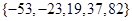 中,则
中,则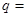 ( )
( )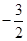
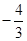
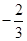
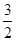
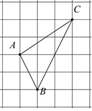
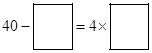 中,在方框中填入两个正整数,使它们的乘积最大.
中,在方框中填入两个正整数,使它们的乘积最大. ____________.
____________.
 的内角
的内角 所对的边为
所对的边为 ,且有
,且有 .
. 的大小;
的大小; ,
, ,
, 为
为 的中点,求
的中点,求 的长.
的长. 满足:
满足: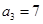 ,
,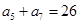 .
.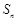 .
.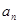 及
及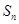 ;
;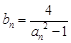 (
( ),求数列
),求数列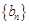 的前n项和
的前n项和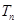 .
.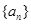 满足
满足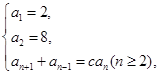 (
( 为常数,
为常数,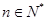 ).
). 时,求
时,求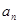 ;
;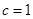 时,求
时,求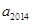 的值;
的值;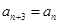 恒成立的常数
恒成立的常数 粤公网安备 44130202000953号
粤公网安备 44130202000953号