江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
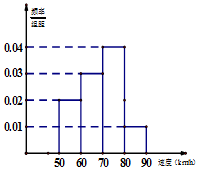
交通部门对某路段公路上行驶的汽车速度实施监控,从速度在 的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在
的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在 以下的汽车有 辆.
以下的汽车有 辆.
来源:2016届江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
若随机安排甲乙丙三人在3天节日中值班,每人值班1天,则甲与丙都不在第一天的概率为 .
来源:2016届江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
如图,在四棱锥 中,已知底面
中,已知底面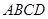 为矩形,
为矩形, 平面
平面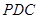 ,点
,点 为棱
为棱 的中点,求证:
的中点,求证:
(1) 平面
平面 ;
;
(2)平面 平面
平面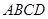 .
.
来源:2016届江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
如图,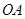 是南北方向的一条公路,
是南北方向的一条公路,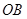 是北偏东
是北偏东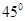 方向的一条公路,某风景区的一段边界为曲线
方向的一条公路,某风景区的一段边界为曲线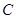 .为方便游客光,拟过曲线
.为方便游客光,拟过曲线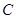 上的某点分别修建与公路
上的某点分别修建与公路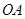 ,
,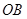 垂直的两条道路
垂直的两条道路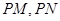 ,且
,且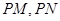 的造价分别为
的造价分别为 万元/百米,
万元/百米, 万元/百米,建立如图所示的直角坐标系
万元/百米,建立如图所示的直角坐标系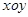 ,则曲线符合函数
,则曲线符合函数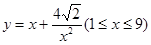 模型,设
模型,设 ,修建两条道路
,修建两条道路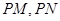 的总造价为
的总造价为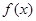 万元,题中所涉及的长度单位均为百米.
万元,题中所涉及的长度单位均为百米.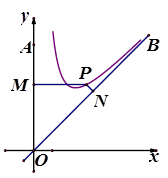
(1)求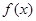 解析式;
解析式;
(2)当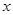 为多少时,总造价
为多少时,总造价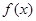 最低?并求出最低造价.
最低?并求出最低造价.
来源:2016届江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
已知各项均为正数的数列 的首项
的首项 ,
, 是数列
是数列 的前n项和,且满足:
的前n项和,且满足: .
.
(1)若 ,
, ,
, 成等比数列,求实数
成等比数列,求实数 的值;
的值;
(2)若 ,求
,求 .
.
来源:2016届江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
如图,在平面直角坐标系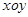 中,已知椭圆
中,已知椭圆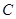 :
: 的离心率
的离心率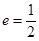 ,左顶点为
,左顶点为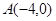 ,过点
,过点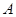 作斜率为
作斜率为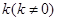 的直线
的直线 交椭圆
交椭圆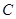 于点
于点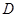 ,交
,交 轴于点
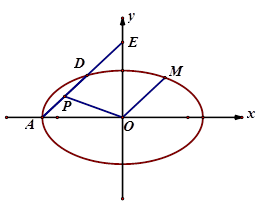
轴于点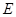 .
.
(1)求椭圆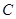 的方程;
的方程;
(2)已知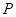 为
为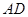 的中点,是否存在定点
的中点,是否存在定点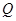 ,对于任意的
,对于任意的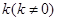 都有
都有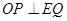 ,若存在,求出点
,若存在,求出点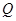 的坐标;若不存在说明理由;
的坐标;若不存在说明理由;
(3)若过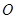 点作直线
点作直线 的平行线交椭圆
的平行线交椭圆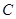 于点
于点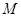 ,求
,求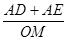 的最小值.
的最小值.
来源:2016届江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
已知函数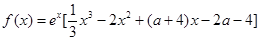 ,其中
,其中 ,
,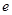 为自然对数的底数
为自然对数的底数
(1)若函数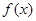 的图像在
的图像在 处的切线与直线
处的切线与直线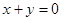 垂直,求
垂直,求 的值.
的值.
(2)关于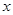 的不等式
的不等式 在
在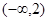 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
(3)讨论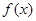 极值点的个数.
极值点的个数.
来源:2016届江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
如图,在直三棱柱 中,底面
中,底面 是直角三角形,
是直角三角形, ,点
,点 是棱
是棱 上一点,满足
上一点,满足 .
.
(1)若 ,求直线
,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(2)若二面角 的正弦值为
的正弦值为 ,求
,求 的值.
的值.
来源:2016届江苏省淮安、宿迁、连云港、徐州苏北四市高三上期末数学试卷
 ,
, ,若
,若 ,则实数
,则实数 的值为 .
的值为 .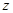 满足
满足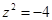 ,若
,若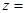 .
.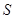 为 .
为 .

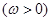 的部分图像如图所示,若
的部分图像如图所示,若 ,则
,则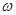 的值为 .
的值为 .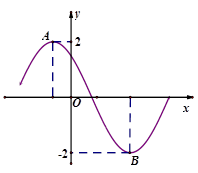
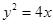 的焦点到双曲线
的焦点到双曲线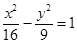 渐近线的距离为 .
渐近线的距离为 .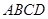 的边
的边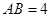 ,
,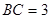 若沿对角线
若沿对角线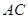 折叠,使得平面
折叠,使得平面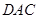
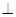 平面
平面 ,则三棱锥
,则三棱锥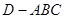 的体积为 .
的体积为 .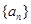 满足
满足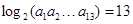 ,等差数列
,等差数列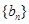 满足
满足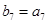 ,则
,则 的值为 .
的值为 . 上的奇函数
上的奇函数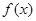 满足当
满足当 时,
时,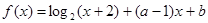 (
( ,
,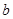 为常数),若
为常数),若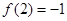 ,则
,则 的值为 .
的值为 .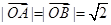 ,且
,且 ,若点
,若点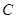 满足
满足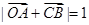 ,则
,则 的取值范围是 .
的取值范围是 . ,若关于
,若关于 的不等式
的不等式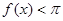 的解集为
的解集为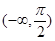 ,则实数
,则实数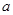 的取值范围是 .
的取值范围是 . ,
, ,
, ,点
,点 是直线
是直线 上的动点,若
上的动点,若 恒成立,则最小正整数
恒成立,则最小正整数 的值为 .
的值为 . 是正实数,满足
是正实数,满足 ,则
,则 的最小值为 .
的最小值为 .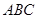 中,角
中,角 的对边为
的对边为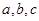 ,已知
,已知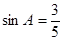 ,
,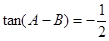 ,
, ;
;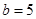 ,求
,求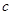 .
. 是直角,圆
是直角,圆 与射线
与射线 相切于点
相切于点 ,与射线
,与射线 相交于两点
相交于两点 .求证:
.求证: 平分
平分 .
.
 ,求矩阵
,求矩阵 的特征值和特征向量.
的特征值和特征向量. 的极坐标方程为
的极坐标方程为 ,已知
,已知 ,
, 为圆
为圆 面积的最小值.
面积的最小值. 均为正数,且
均为正数,且 ,求证:
,求证: .
. 满足
满足 ,
, .
. ;
;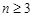 时,
时, .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号