高中数学多面角及多面角的性质试题

已知函数，钝角（角对边为）的角满足.
（1）求函数的单调递增区间；
（2）若，求.

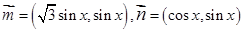已知向量，函数．
（1）求函数的最小正周期及单调递增区间；
（2）已知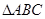中,角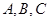的对边分别为，若，，
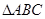求的面积.

（本小题满分12分）
已知三个内角的对边分别为，的图象与直线相切，且切点横坐标依次成公差为的等差数列，点是函数的一个对称中心．
（Ⅰ）求的大小；
（Ⅱ）已知，为的面积，求的最大值及此时B的值．

设向量，，
（1）若，求的值；
（2）设函数，求的最大值。

如图所示，某市政府决定在以政府大楼为中心，正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地，并考虑与周边环境协调，设计要求该图书馆底面矩形的四个顶点都要在边界上，图书馆的正面要朝市政府大楼.设扇形的半径 ，，与之间的夹角为.

（1）将图书馆底面矩形的面积表示成的函数.
（2）求当为何值时，矩形的面积有最大值？其最大值是多少？(用含R的式子表示)

设平面向量＝，，，，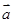
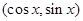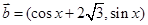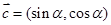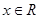⑴若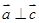，求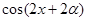的值；（2）若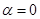，求函数的最大值，并求出相应的值．

函数是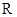上的增函数且，其中是锐角，并且使得函数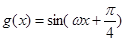在上单调递减，则的取值范围是（   ）

A．

B．

C．

D．

已知向量，，且．
（1）将表示为的函数，并求的单调递增区间；
（2）已知分别为的三个内角对应的边长，若，且，，求的面积．

M、N是曲线y=πsinx与曲线y=πcosx的两个不同的交点,则|MN|的最小值为(　　)

A．π

B．π

C．π

D．2π

已知函数f(x)＝2sin xcos x＋2cos²x－，x∈R.
(1)求函数f(x)的最小正周期；
(2)在锐角△ABC中，若f(A)＝1，·＝，求△ABC的面积．

设函数f(x)＝＋2cos²x.
(1)求f(x)的最大值，并写出使f(x)取最大值时x的集合；
(2)已知△ABC中，角A，B，C的对边分别为a，b，c，若f(B＋C)＝，b＋c＝2，求a的最小值．

关于函数f(x)＝4sin(2x＋), (x∈R)有下列命题：
①y＝f(x)是以2π为最小正周期的周期函数；
② y＝f(x)可改写为y＝4cos(2x－)；
③y＝f(x)的图象关于(－，0)对称；
④ y＝f(x)的图象关于直线x＝－对称；
其中正确的序号为               。

已知函数的图象经过点.
（1）求实数的值；
（2）求函数的最小正周期与单调递增区间.

设函数f(x)=msinx+cosx(x∈R)的图象经过点(,1).
(1)求f(x)的解析式,并求函数的最小正周期.
(2)若f(α+)=且α∈(0,),求f(2α-)的值.

函数f(x)=sin2x--.
(1)若x∈[,],求函数f(x)的最值及对应的x的值.
(2)若不等式[f(x)-m]²<1在x∈[,]上恒成立,求实数m的取值范围.