已知函数f(x)=sinx+cosx.
(1)若f(x)=2f(﹣x),求 的值;
的值;
(2)求函数F(x)=f(x)•f(﹣x)+f2(x)的最大值和单调递增区间.
关于函数f(x)=4sin(2x+ ),(x∈R)有下列命题:
),(x∈R)有下列命题:
①y=f(x)是以2π为最小正周期的周期函数;
②y=f(x)可改写为y=4cos(2x﹣ );
);
③y=f(x)的图象关于点(﹣ ,0)对称;
,0)对称;
④y=f(x)的图象关于直线x= 对称;
对称;
其中正确的序号为 .
已知函数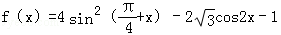 ,且给定条件p:“
,且给定条件p:“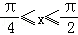 ”,
”,
(1)求f(x)的最大值及最小值
(2)若又给条件q:“|f(x)﹣m|<2“且p是q的充分条件,求实数m的取值范围.
函数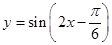 的图像与函数
的图像与函数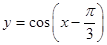 的图像()
的图像()
| A.有相同的对称轴但无相同的对称中心 |
| B.有相同的对称中心但无相同的对称轴 |
| C.既有相同的对称轴也有相同的对称中心 |
| D.既无相同的对称中心也无相同的对称轴 |
有下列命题:
①在函数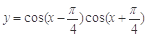 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为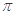 ;
;
②命题:“若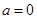 ,则
,则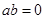 ”的否命题是“若
”的否命题是“若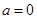 ,则
,则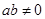 ”;
”;
③“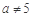 且
且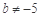 ”是“
”是“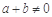 ”的必要不充分条件;
”的必要不充分条件;
④已知命题p:对任意的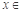 R,都有
R,都有 ,则
,则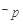 是:存在
是:存在 ,使得
,使得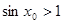 ;
;
⑤命题“若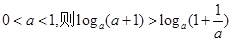 ”是真命题;
”是真命题;
⑥在△ABC中,若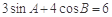 ,
,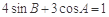 ,则角C等于
,则角C等于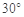 或
或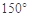 .
.
其中所有真命题的序号是 .
已知向量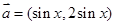 ,
,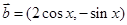 ,函数
,函数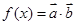 .
.
(1)求函数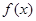 的最小正周期;
的最小正周期;
(2)求函数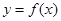 在
在 上的值域.
上的值域.