有下列命题:①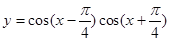 的图象中相邻两个对称中心的距离为
的图象中相邻两个对称中心的距离为 ,②
,② 的图象关于点
的图象关于点 对称,③关于
对称,③关于 的方程
的方程 有且仅有一个实根,则
有且仅有一个实根,则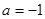 ,④命题
,④命题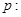 对任意
对任意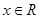 ,都有
,都有 ;则
;则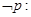 存在
存在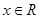 ,使得
,使得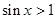 .其中真命题的序号是_________________________ .
.其中真命题的序号是_________________________ .
已知函数 ,
, .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在区间
在区间 上的值域.
上的值域.
受日月引力影响,海水会发生涨退潮现象.通常情况下,船在涨潮时驶进港口,退潮时离开港口.某港口在某季节每天港口水位的深度 (米)是时间
(米)是时间 (
( ,单位:小时,
,单位:小时, 表示0:00—零时)的函数,其函数关系式为
表示0:00—零时)的函数,其函数关系式为

 .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
.已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
(1)试求函数 的表达式;
的表达式;
(2)某货船的吃水深度(船底与水面的距离)为7米,安全条例规定船舶航行时船底与海底的距离不小于3.5米是安全的,问该船在当天的什么时间段能够安全进港?若该船欲于当天安全离港,则它最迟应在当天几点以前离开港口?
(本小题满分12分)定义在区间 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时函数
时函数 图象如图所示.
图象如图所示.
(1)求函数 在
在 的表达式;
的表达式;
(2)求方程 的解;
的解;
(3)是否存在常数 的值,使得
的值,使得 在
在 上恒成立;若存在,求出
上恒成立;若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
设函数 .
.
(1) 写出函数的最小正周期及单调递减区间;
(2) 当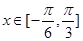 时,函数
时,函数 的最大值与最小值的和为
的最大值与最小值的和为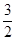 ,求
,求 的解析式;
的解析式;
(3) 将满足(2)的函数 的图像向右平移
的图像向右平移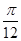 个单位,纵坐标不变,横坐标伸长为原来的2倍,再向下平移
个单位,纵坐标不变,横坐标伸长为原来的2倍,再向下平移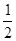 个单位,得到函数
个单位,得到函数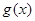 ,求
,求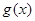 图像与
图像与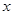 轴的正半轴、直线
轴的正半轴、直线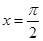 所围成图形的面积.
所围成图形的面积.
已知函数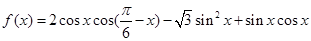 .
.
(1)求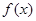 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)设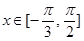 ,求
,求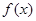 的值域.
的值域.
函数 的一段图象如图5所示:将
的一段图象如图5所示:将 的图像向右平移
的图像向右平移 个单位,可得到函数
个单位,可得到函数 的图象,且图像关于原点对称,
的图象,且图像关于原点对称, .
.
(1).求 的值;
的值;
(2).求 的最小值,并写出
的最小值,并写出 的表达式;
的表达式;
(3).若关于 的函数
的函数 在区间
在区间 上最小值为
上最小值为 ,求实数
,求实数 的取值范围.
的取值范围.
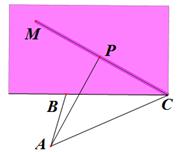
如图,某人在垂直于水平地面的墙面前的点
处进行射击训练,已知点
到墙面的距离为
,某目标点
沿墙面上的射线
移动,此人为了准确瞄准目标点
,需计算由点
观察点
的仰角
的大小(仰角
为直线
与平面
所成的角),若
,
,
,则
的最大值是( )
| A. |
|
B. |
|
C. |
|
D. |
|
设函数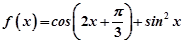 .
.
(1)求函数f(x)的最大值和最小正周期。
(2)设A、B、C为⊿ABC的三个内角,若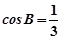 ,
, ,且C为锐角,求
,且C为锐角,求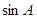 .
.
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,下列结论:
①最小正周期为π;
②将f(x)的图象向左平移 个单位,所得到的函数是偶函数;
个单位,所得到的函数是偶函数;
③f(0)=1;
④f( )<f(
)<f( );
);
⑤f(x)=-f( -x).
-x).
其中正确的是( )
| A.①②③ | B.②③④ | C.①④⑤ | D.②③⑤ |
已知函数 (
( ,
, ,
, ),
), 的部分图像如图所示,
的部分图像如图所示,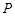 、
、 分别为该图像的最高点和最低点,点
分别为该图像的最高点和最低点,点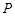 的坐标为
的坐标为 .
.
(1)求 的最小正周期及
的最小正周期及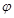 的值;
的值;
(2)若点 的坐标为
的坐标为 ,
,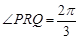 ,求
,求 的值和
的值和 的面积.
的面积.