(本小题满分13分)已知函数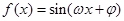 (
( ,
, )图象的相邻两对称轴间的距离为
)图象的相邻两对称轴间的距离为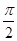 ,若将函数
,若将函数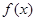 的图象向左平移
的图象向左平移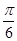 个单位后图象关于
个单位后图象关于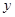 轴对称.
轴对称.
(1)求使 成立的
成立的 的取值范围;
的取值范围;
(2)设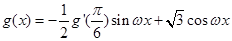 ,其中
,其中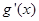 是
是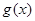 的导函数,若
的导函数,若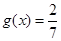 ,且
,且 ,求
,求 的值.
的值.
已知点P(x1,y1),Q(x2,y2)是函数f(x)=sin(ωx+Φ)(ω>0,0<Φ<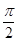 )图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为
)图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为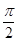 ,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
(1)求函数f(x)的解析式;
(2)求g(B)= f(B)+f(B+
f(B)+f(B+ )的取值范围.
)的取值范围.
已知函数 的最大值为
的最大值为 .
.
(Ⅰ)求常数 的值;
的值;
(Ⅱ)求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)若将 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
已知函数f(x)=4cos2x﹣4 sinxcosx﹣2(x∈R).
sinxcosx﹣2(x∈R).
(1)求函数f(x)的单调递增区间;
(2)设△ABC的内角A,B,C对应边分别为a、b、c,且c=3,f(C)=﹣4,若向量 =(1,sinA)与向量
=(1,sinA)与向量 =(1,2sinB)共线,求a、b的值.
=(1,2sinB)共线,求a、b的值.
已知函数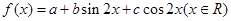 的图像过点
的图像过点 ,且b>0,又
,且b>0,又 的最大值为
的最大值为 .
.
(Ⅰ)将 写成含
写成含 的形式;
的形式;
(Ⅱ)由函数y = 图像经过平移是否能得到一个奇函数y =
图像经过平移是否能得到一个奇函数y = 的图像?若能,请写出平移的过程;若不能,请说明理由。
的图像?若能,请写出平移的过程;若不能,请说明理由。
已知函数f(x)=cos(2x+ )+sin2x
)+sin2x
(1)求函数f(x)的单调递减区间及最小正周期;
(2)设锐角△ABC的三内角A,B,C的对边分别是a,b,c,若c= ,cosB=
,cosB= ,f(
,f( )=-
)=- ,求b.
,求b.