四川省成都市新都区高三诊断测试理科数学试卷
已知全集U=R,集合A={x|x2-2x<0},B={x|x-1≥0},那么集合A∩ðUB=( )
| A.{x|0<x<1} | B.{x|x<0} | C.{x|x>2} | D.{x|1<x<2} |
等差数列{an}的前n项和为Sn,若a1<0,且S2015=0,则当Sn取得最小值时,n的取值为( )
| A.1009 | B.1008 | C.1007或1008 | D.1008或1009 |
在△ABC中,三内角A,B,C成等差数列,b=6,则△ABC的外接圆半径为( )
| A.6 | B.12 | C.2 |
D.4 |
设f(x)=4sinxsin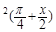 +cos2x,|f(x)-m|<3对"x∈(0,π)恒成立,则实数m的范围是( )
+cos2x,|f(x)-m|<3对"x∈(0,π)恒成立,则实数m的范围是( )
| A.[0,4] | B.(0,4] | C.[0,4) | D.(0,4) |
设p:(x-2)(y-5)≠0;q:x≠2或y≠5;r:x+y≠7;则下列命题:
①p是r的既不充分也不必要条件;②p是q的充分不必要条件;③q是r的必要不充分条件.
其中全部真命题有( )
| A.①② | B.①③ | C.②③ | D.①②③ |
已知x,y∈(0,1),且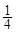 lnx,
lnx,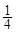 ,lny成等比数列,则xy有( )
,lny成等比数列,则xy有( )
| A.最小值e | B.最小值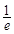 |
C.最大值e | D.最大值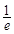 |
△ABC中,|AB|=10,|AC|=15,∠BAC= ,点D是边AB的中点,点E在直线AC上,且
,点D是边AB的中点,点E在直线AC上,且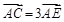 ,直线CD与BE相交于点P,则线段AP的长为( )
,直线CD与BE相交于点P,则线段AP的长为( )
A.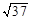 |
B. |
C.2 |
D.2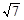 |
函数f1(x)=x3,f2(x)= ,f3(x)=
,f3(x)= ,f4(x)=
,f4(x)=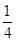 |sin(2πx)|,等差数列{an}中,a1=0,a2015=1,bn=|fk(an+1)-fk(an)|(k=1,2,3,4),用Pk表示数列{bn}的前2014项的和,则( )
|sin(2πx)|,等差数列{an}中,a1=0,a2015=1,bn=|fk(an+1)-fk(an)|(k=1,2,3,4),用Pk表示数列{bn}的前2014项的和,则( )
| A.P4<1=P1=P2<P3=2 | B.P4<1=P1=P2<P3<2 |
| C.P4=1=P1=P2<P3=2 | D.P4<1=P1<P2<P3=2 |
德国著名数学家狄利克雷在数学领域成就显著,以其命名的函数f(x)=被称为狄利克雷函数,其中R为实数集,Q为有理数集,则关于函数f(x)有如下四个命题:
①f(f(x))=0;
②函数f(x)是偶函数;
③f(x)是周期函数;
④存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为等边三角形;
⑤存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为直角三角形.
其中真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
数列{an}的前n项和为Sn,且满足an+2=an+1-an(n∈N*),a1=1,a2=2,则S2014=_________.
已知函数f(x)是定义在R上的奇函数,且对任意x∈R,有f(x-3)=f(x-5),若当x∈[0,1)时,f(x)=2x-1,则f(1)+f(log 6)的值为___________
6)的值为___________
△ABC中,角A,B,C的对边分别为a,b,c,已知b=8,c=6,A= ,∠BAC的角平分线交边BC于点D,则|AD|=___________.
,∠BAC的角平分线交边BC于点D,则|AD|=___________.
函数f(x)=10x+x-7与g(x)=lgx+x-7的零点分别为1和x2,则x1+x2=_______
定义一:对于一个函数f(x)(x∈D),若存在两条距离为d的直线y=kx+m1和y=kx+m2,使得在x∈D时,kx+m1≤f(x)≤kx+m2恒成立,则称函数f(x)在D内有一个宽度为d的.
定义二:若一个函数f(x),对于任意给定的正数ɛ,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ɛ的,则称f(x)在正无穷处有.下列函数:
①f(x)=lgx,②f(x)= ,③f(x)=-
,③f(x)=- ,④f(x)=
,④f(x)= ,⑤f(x)=2x,⑥f(x)=3x-
,⑤f(x)=2x,⑥f(x)=3x-
其中在正无穷处有的函数的序号是___________.
已知点P(x1,y1),Q(x2,y2)是函数f(x)=sin(ωx+Φ)(ω>0,0<Φ<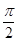 )图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为
)图象上的任意两点,若|y1-y2|=2时,|x1-x2|的最小值为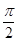 ,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
,且函数f(x)的图象经过点(0,2),在△ABC中,角A,B,C的对边分别为a,b,c,且2sinAsinC+cos2B=1.
(1)求函数f(x)的解析式;
(2)求g(B)= f(B)+f(B+
f(B)+f(B+ )的取值范围.
)的取值范围.
设在一个盒子中,放有标号为1,2,3的三张卡片,现从这个盒子里有放回地先后抽得两张卡片,标号分别记为x,y,设随机变量ξ=|x-2|+|y-x|
(1)写出随机变量ξ的取值集合(直接写出答案即可);
(2)求ξ的分布列和数学期望及方差.
如图,多边形ABCDE中,∠ABC=90°,AD∥BC,△ADE是正三角形,AD=2,AB=BC=1,沿直线AD将△ADE折起至△ADP的位置,连接PB,BC,构成四棱锥P-ABCD,使得PB= .点O为线段AD的中点,连接PO.
.点O为线段AD的中点,连接PO.
(1)求证:PO⊥平面ABCD;
(2)求二面角B-PC-D的大小的余弦值.
数列{an}的前n项和为Sn,若3Sn+an=3n+2(n∈N*),数列{bn}满足2bn+1=bn+bn+2(n∈N*),且b3=7,b8=22.
(1)求数列{an}和{bn}的通项公式an和bn;
(2)设数列cn=anbn,求{cn}的前n项和Tn.
已知函数f(x)= +lnx.
+lnx.
(1)若函数f(x)在[1,+∞)上为增函数,求实数a的取值范围;
(2)设数列{bn}的前n项和为Sn,其中bn= ,求证:当n≥2时,1+lnn>Sn.
,求证:当n≥2时,1+lnn>Sn.
 (其中i为虚数单位),则
(其中i为虚数单位),则 的值为( )
的值为( )



 ax2-(a+1)x(a∈R).
ax2-(a+1)x(a∈R). 粤公网安备 44130202000953号
粤公网安备 44130202000953号