如图,多边形ABCDE中,∠ABC=90°,AD∥BC,△ADE是正三角形,AD=2,AB=BC=1,沿直线AD将△ADE折起至△ADP的位置,连接PB,BC,构成四棱锥P-ABCD,使得PB=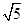 .点O为线段AD的中点,连接PO.
.点O为线段AD的中点,连接PO.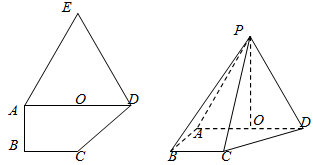
(1)求证:PO⊥平面ABCD;
(2)求二面角B-PC-D的大小的余弦值.
相关知识点
推荐套卷
如图,多边形ABCDE中,∠ABC=90°,AD∥BC,△ADE是正三角形,AD=2,AB=BC=1,沿直线AD将△ADE折起至△ADP的位置,连接PB,BC,构成四棱锥P-ABCD,使得PB=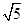 .点O为线段AD的中点,连接PO.
.点O为线段AD的中点,连接PO.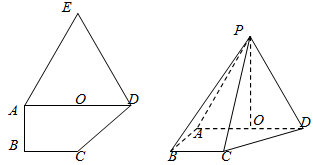
(1)求证:PO⊥平面ABCD;
(2)求二面角B-PC-D的大小的余弦值.