已知函数f（x）＝lnx＋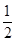
ax2－（a＋1）x（a∈R）.
（1）当a＝1时，求曲线y＝f（x）在点（1，f（1））处的切线方程；
（2）当a＞0时，若f（x）在区间[1，e]上的最小值为－2，求实数a的值；
（3）若对"x1，x2∈（0，＋∞），x1＜x2，且f（x1）＋x1＜f（x2）＋x2恒成立，求实数a的取值范围.
中，
是
的中点，
．
；
的距离；
与平面
的位置关系，并证明你的结论．
中，
，
，
，点
在
上，且
．
平面
；
为棱，
与
为面的二面角的大小．
中，
，
，求证：
．
，
平面
，如图．求证：直线
与平面
相交．
推荐套卷
已知函数f（x）＝lnx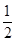＋ax2－（a＋1）x（a∈R）.
（1）当a＝1时，求曲线y＝f（x）在点（1，f（1））处的切线方程；
（2）当a＞0时，若f（x）在区间[1，e]上的最小值为－2，求实数a的值；
（3）若对"x1，x2∈（0，＋∞），x1＜x2，且f（x1）＋x1＜f（x2）＋x2恒成立，求实数a的取值范围.
粤公网安备 44130202000953号