(本小题满分12分)已知数列 ,
,
定义其倒均数是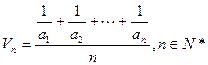 。
。
(1)求数列{ }的倒均数是
}的倒均数是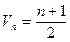 ,求数列{
,求数列{ }的通项公式
}的通项公式 ;
;
(2)设等比数列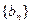 的首项为-1,公比为
的首项为-1,公比为 ,其倒数均为
,其倒数均为 ,若存在正整数k,使得当
,若存在正整数k,使得当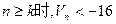 恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
推荐套卷
(本小题满分12分)已知数列 ,
,
定义其倒均数是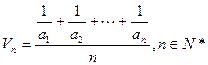 。
。
(1)求数列{ }的倒均数是
}的倒均数是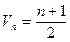 ,求数列{
,求数列{ }的通项公式
}的通项公式 ;
;
(2)设等比数列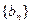 的首项为-1,公比为
的首项为-1,公比为 ,其倒数均为
,其倒数均为 ,若存在正整数k,使得当
,若存在正整数k,使得当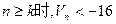 恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)