曲线 与直线
与直线 在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3, ,则|P2P4|=________.
在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3, ,则|P2P4|=________.
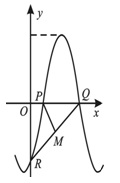
(本小题满分12分)如图,函数 (其中
(其中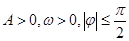 )的图象与坐标轴的三个交点为
)的图象与坐标轴的三个交点为 ,且
,且 ,
,
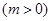 ,
, ,
,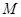 为
为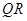 的中点,
的中点,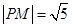 .
.
(Ⅰ)求 的值及
的值及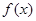 的解析式;
的解析式;
(Ⅱ)设 ,求
,求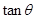 .
.
【改编】已知函数 若
若 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
| A.(1,2014) | B.(1,2015) | C.(2,2015) | D.[2,2015] |
已知函数 的部分图象如图所示,
的部分图象如图所示, 是图象的最高点,
是图象的最高点, 为图象与
为图象与 轴的交点,
轴的交点, 为坐标原点,若
为坐标原点,若

(1)求函数 的解析式,
的解析式,
(2)将函数 的图象向右平移2个单位后得到函数
的图象向右平移2个单位后得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的值域.
的值域.
【改编题】已知函数 的图象在
的图象在 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 在区间
在区间 上的最大值与最小值.
上的最大值与最小值.
已知函数 .
.
(1)求函数的最小正周期、最大值及取最大值时自变量的取值集合;
(2)在△ABC中,角A,B,C的对边分别是a,b,c;若a,b,c成等比数列,且 ,求
,求 的值.
的值.
某同学用“五点法”画函数 在某一个周期的图象时,列表并填入的部分数据如下表:
在某一个周期的图象时,列表并填入的部分数据如下表:
(1)求 ,
, ,
, 的值及函数
的值及函数 的表达式;
的表达式;
(2)将函数 的图象向左平移
的图象向左平移 个单位,可得到函数
个单位,可得到函数 的图象,求函数
的图象,求函数 在区间
在区间 的最小值.
的最小值.
(本小题12分)已知函数 .
.
(Ⅰ)当 时,把
时,把 的图像向右平移
的图像向右平移 个单位得到函数
个单位得到函数 的图像,求函数
的图像,求函数 的图像的对称中心坐标;
的图像的对称中心坐标;
(Ⅱ)设 ,若
,若 的图象与直线
的图象与直线 的相邻两个交点之间的距离为π,求
的相邻两个交点之间的距离为π,求 的值,并求函数
的值,并求函数 的单调递增区间.
的单调递增区间.
已知函数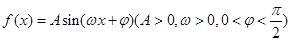 部分图象如图所示。
部分图象如图所示。
(1)求函数 的解析式;
的解析式;
(2)当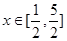 时,求函数
时,求函数 的值域。
的值域。
【改编】(本小题满分12分)已知函数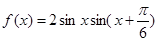 .
.
(1)当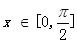 时,求函数
时,求函数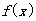 的最大值;
的最大值;
(2)当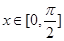 时,求函数
时,求函数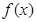 的单调增区间;
的单调增区间;
设函数
(Ⅰ)求 的最小正周期及值域;
的最小正周期及值域;
(Ⅱ)已知 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,求
,求 的面积.
的面积.
本题共有2小题,第(1)小题满分6分,第(2)小题满分6分.
已知函数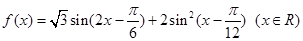 .
.
(1)化简并求函数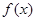 的最小正周期;
的最小正周期;
(2)求使函数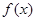 取得最大值的
取得最大值的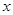 集合.
集合.