高中数学多面角及多面角的性质试题

（本小题满分12分）已知函数（）在时有最小值．
（Ⅰ）求的值；
（Ⅱ）在中，，，分别是角，，所对的边，已知，，，求角的值．

设函数，若对于任意的实数x，都有，求实数a的范围．

已知函数的部分图象如图所示．

（1）求函数的解析式；
（2）将函数的图象做怎样的平移变换可以得到函数的图象；
（3）若方程上有两个不相等的实数根，求m的取值范围．

（本题12分）已知定义在区间上的函数的图像关于直线对称，当时，函数．
（1）求的值；
（2）求的表达式；
（3）若关于的方程有解，那么将方程在取某一确定值时所求得的所有解的和记为，求的所有可能取值及相应的的取值范围．

（本小题满分10分）已知函数，且当时，的最小值为2，
（1）求的单调递增区间；
（2）先将函数的图象上的点纵坐标不变，横坐标缩小到原来的，再把所得的图象向右平移个单位，得到函数的图象，求方程在区间上所有根之和．

（本小题满分12分）已知，，且函数
（1）设方程在内有两个零点，求的值；
（2）若把函数的图像向左平移个单位，再向上平移2个单位，得函数图像，求函数在上的单调增区间．

（本小题满分13分）函数y＝Asin（ωx+）（A＞0，ω＞0）在x∈（0，7π）内取到一个最大值和一个最小值，且当x＝
π时，y有最大值3，当x＝6π时，y有最小值-3．
（1）求此函数解析式；
（2）写出该函数的单调递增区间；
（3）是否存在实数m，满足不等式Asin（）＞Asin（）?若存在，求出m值（或范围），若不存在，请说明理由．

（本小题满分12分）已知函数f （x）＝Asin（ωx＋φ） （A>0，ω>0，|φ|<）在一个周期内的图象如图所示．

（1）求函数的解析式；
（2）设0<x<π，且方程f （x）＝m有两个不同的实数根，求实数m的取值范围以及这两个根的和．

（本小题满分10分）已知函数，且当时，的最小值为2，
（1）求的单调递增区间；
（2）先将函数的图象上的点纵坐标不变，横坐标缩小到原来的，再把所得的图象向右平移个单位，得到函数的图象，求方程在区间上所有根之和．

已知函数f（x）=﹣3x﹣x³，x∈R，若时，不等式f（cos²θ﹣2t）+f（4sinθ﹣3）≥0恒成立，则实数t的取值范围是      ．

（本小题13分）已知函数的一系列对应值如下表：

 
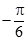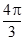（1）根据表格提供的数据求函数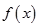的解析式；
（2）求函数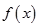的单调递增区间和对称中心；
（3）若当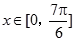时，方程恰有两个不同的解，求实数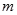的取值范围．

（本小题满分12分）
已知函数
（1）求函数的最大值，以及取到最大值时所对应的的集合；
（2）在上恒成立，求实数的取值范围。

已知函数，给出下列四个说法：
①为奇函数；
②的一条对称轴为；
③的最小正周期为；
④在区间上单调递增；
⑤的图象关于点成中心对称．
其中正确说法的序号是            ．

已知函数的周期为 ，图像的一个对称中心为，将函数图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得到的图像向右平移个单位长度后得到函数的图像．
（1）求函数与的解析式；
（2）若 ，是第一象限的角，且 ，求 的值．

给出下列四个结论：
①存在实数，使
②函数是偶函数
③直线 是函数的一条对称轴方程
④若都是第一象限的角，且，则
其中正确结论的序号是____________________．（写出所有正确结论的序号）