某同学用“五点法”画函数 在某一个周期的图象时,列表并填入了部分数据,如下表:
在某一个周期的图象时,列表并填入了部分数据,如下表:
(1)请求出上表中的 ,
, ,
,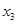 ,并直接写出函数f(x)的解析式;
,并直接写出函数f(x)的解析式;
(2)将f(x)的图象沿x轴向右平移 个单位得到函数g(x),若函数g(x)在
个单位得到函数g(x),若函数g(x)在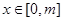 (其中
(其中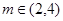 )上的值域为
)上的值域为 ,且此时其图象的最高点和最低点分别为P,Q,求
,且此时其图象的最高点和最低点分别为P,Q,求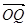 与
与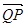 夹角
夹角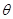 的大小.
的大小.
已知函数f(x)=2sinωxcosωx﹣2 sin2ωx+
sin2ωx+ (ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为
(ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为 .
.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调增区间;
(Ⅲ)若f(α)= ,求sin(
,求sin( π﹣4α)的值.
π﹣4α)的值.
函数 的图象如下图所示,为了得到
的图象如下图所示,为了得到 的图像,可以将
的图像,可以将 的图像 ()
的图像 ()
A.向右平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
已知命题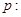
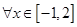 ,函数
,函数 的值大于
的值大于 .若
.若 是真命题,则命题
是真命题,则命题 可以是()
可以是()
A.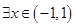 ,使得 ,使得 |
B.“ ”是“函数 ”是“函数 在区间 在区间 上有零点”的必要不充分条件 上有零点”的必要不充分条件 |
C.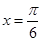 是曲线 是曲线 的一条对称轴 的一条对称轴 |
D.若 ,则在曲线 ,则在曲线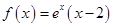 上任意一点处的切线的斜率不小于 上任意一点处的切线的斜率不小于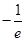 |
已知函数 (其中
(其中 为常数,且
为常数,且 )的部分图像如图所示.
)的部分图像如图所示.
(1)求函数 的解析式
的解析式
(2)若 求
求 的值
的值
已知函数 的最大值为3,函数
的最大值为3,函数 的图象上相邻两对称轴间的距离为
的图象上相邻两对称轴间的距离为 ,且
,且 .
.
(1)求函数 的解析式;
的解析式;
(2)将 的图象向左平移
的图象向左平移 个单位,再向下平移1个单位后得到函数
个单位,再向下平移1个单位后得到函数 的图象,试判断
的图象,试判断 的奇偶性,并求出
的奇偶性,并求出 在R上的单调递增区间.
在R上的单调递增区间.
如图,在平面直角坐标系 中,
中, ,
, ,
, .
.
(1)求 的面积;
的面积;
(2)若函数
 的图象经过
的图象经过 、
、 、
、 三点,且
三点,且 、
、 为
为 的图象与
的图象与 轴相邻的两个交点,求
轴相邻的两个交点,求 的解析式.
的解析式.
已知函数 (
( ),相邻两对称轴之间的距离为
),相邻两对称轴之间的距离为 .
.
(1)求函数 的解析式;
的解析式;
(2)把函数 的图象向右平移
的图象向右平移 个单位,再纵坐标不变横坐标缩短到原来的
个单位,再纵坐标不变横坐标缩短到原来的 后得到函数
后得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的单调递增区间.
的单调递增区间.