高中数学多面角及多面角的性质试题

（本小题满分14分）已知函数的图像过点且关于直线对称，图像上相邻两个最高点的距离为
（Ⅰ）求的值；
（Ⅱ）若，求的值．

已知函数 .
（Ⅰ）求函数的单调增区间；  
（Ⅱ）在中，内角所对边分别为，，若对任意的不等式恒成立，求面积的最大值．

已知函数，则下列命题正确的是            .（填上你认为正确的所有命题的序号）
①函数的最大值为2;
②函数的图象关于点对称;
③函数的图象与函数的图象关于轴对称;
④若实数使得方程在上恰好有三个实数解，则;
⑤设函数，若，则.

（本小题满分12分）已知函数，且当时，的最小值为2，
（1）求的值，并求的单调递增区间；
（2）先将函数的图象上的点纵坐标不变，横坐标缩小到原来的，再将所得的图象向右平移个单位，得到函数的图象，求方程在区间上所有根之和.

（本小题满分12分）设向量，，。
（1）求的最小正周期；
（2）求在区间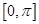上的单调递减区间.

（本小题满分13分）已知向量 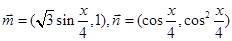，记
（Ⅰ）若 ，求 的值；
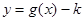（Ⅱ）将函数 的图象向右平移 个单位得到 的图象，若函数 在 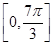上有零点，求实数k的取值范围．

(本小题满分13分)设函数
（Ⅰ）求的最小正周期及值域；
（Ⅱ）已知中，角的对边分别为，若，，，求的面积．

已知函数的最大值为2，是集合中的任意两个元素，且的最小值为．
（1）求函数的解析式及其对称轴；
（2）若，求的值．

（本小题满分12分）已知向量互相平行，其中．
（1）求和的值；
（2）求的最小正周期和单调递增区间.

已知函数, 则的值为（  ）

A．

B．

C．

D．

（本小题满分13分）已知函数, x∈R的部分图象如图所示.

（Ⅰ）求函数的最小正周期和单调递增区间；
（Ⅱ） 设点B是图象上的最高点，点A是图象与x轴的交点，求的值.

已知函数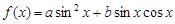满足
（1）求实数的值以及函数的最小正周期；
（2）记，若函数是偶函数，求实数的值.

(本题满分10分)
已知函数.
（1）求函数的最小正周期；
（2）求在上的最大值和最小值．

已知函数f（x）=cosx•sin（x+）﹣cos²x+，x∈R．
（1）求f（x）的最小正周期；
（2）求f（x）在闭区间[﹣，]上的最大值和最小值．

（本小题满分12分）已知函数
（1）求函数的最小正周期和最大值；
（2）设的三内角分别是A、B、C．若，且,求的值．