山东省菏泽市高三第一次模拟考试理科数学试卷

已知复数，则等于（   ）

A．

B．

C．

D．

设集合，则（   ）

A．

B．

C．

D．

给定函数① ② ③ ④，其中在区间上单调递减的函数序号是（   ）

在中，若，则的形状是（   ）

为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（10分制）的频率分布直方图如图所示，假设得分值的中位数为，众数，平均数为，则（    ）

A．	B．
C．	D．

某电视台的一个综艺栏目对六个不同的节目排演出顺序，最前只能排甲或乙，最后不能排甲，则不同的排法共有（   ）

若函数的图象如图所示，则的范围为（  ）

A．

B．

C．

D．

设双曲线的离心率为2，且一个焦点与抛物线的焦点相同，则此双曲线的方程为（  ）

A．

B．

C．

D．

已知函数，若函数在R上有两个零点，则的取值范围是（   ）

A．

B．

C．

D．

若函数，并且，则下列各结论正确的是（   ）

A．

B．

C．

D．

如图，正方体的棱长为1，E为棱上的点，为AB的中点，则三棱锥的体积为        .

已知满足不等式组，则的最大值与最小值的比为        .

定义在实数集R上的函数满足，且，现有以下三种叙述：
①8是函数的一个周期；
②的图象关于直线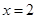对称；
③是偶函数。
其中正确的序号是            .

执行如图中的程序框图，如果输入的，则输出的所在区间是          .

在实数集R中，我们定义的大小关系“＞”为全体实数排了一个“序”．类似的，我们在平面向量集上也可以定义一个称“序”的关系，记为“”．定义如下：对于任意两个向量，“”当且仅当“”或“”。按上述定义的关系“”，给出如下四个命题：
①若，则；
②若，则；
③若，则对于任意；
④对于任意向量，若，则。
其中真命题的序号为__________

（本小题满分12分）已知函数，且当时，的最小值为2，
（1）求的值，并求的单调递增区间；
（2）先将函数的图象上的点纵坐标不变，横坐标缩小到原来的，再将所得的图象向右平移个单位，得到函数的图象，求方程在区间上所有根之和.

（本小题满分12分）如图，将边长为2的正六边形ABCDEF沿对角线BE翻折，连接AC、FD，形成如图所示的多面体，且

（1）证明：平面ABEF平面BCDE；
（2）求平面ABC与平面DEF所成的二面角（锐角）的余弦值.

（本小题满分12分）已知一个袋子里装有只有颜色不同的6个小球，其中白球2个，黑球4个，现从中随机取球，每次只取一球.
（1）若每次取球后都放回袋中，求事件“连续取球四次，至少取得两次白球”的概率；
（2）若每次取球后都不放回袋中，且规定取完所有白球或取球次数达到五次就终止游戏，记游戏结束时一共取球X次，求随机变量X的分布列与期望.

（本小题满分12分）数列的前n项和为，且
（1）求数列的通项公式；
（2）若数列满足：，求数列的通项公式；
（3）令，求数列的 n项和.

（本小题满分13分）已知函数（其中是自然对数的底数），为导函数。
（1）当时，其曲线在点处的切线方程；
（2）若时，都有解，求的取值范围；
（3）若，试证明：对任意恒成立.

（本小题满分14分）已知焦点在轴上的椭圆的离心率为，分别为左右焦点，过点作直线交椭圆于（在两点之间）两点，且，关于原点的对称点为.
（1）求椭圆的方程；
（2）求直线的方程；
（3）过任作一直线交过三点的圆于两点，求面积的取值范围.