已知函数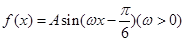 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是 ,且满足,
,且满足,
(1)求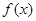 的单调递减区间;
的单调递减区间;
(2)在钝角△ABC中,a、b、c分别为角A、B、C的对边,sinB=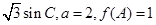 ,求△ABC的面积。
,求△ABC的面积。
如图所示,某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料,已知已有两面墙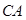 、
、 的夹角为
的夹角为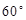 (即
(即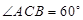 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料 米(两面墙的长均大于
米(两面墙的长均大于 米),为了使得仓库的面积尽可能大,记
米),为了使得仓库的面积尽可能大,记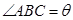 ,问当
,问当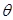 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 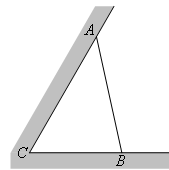
已知向量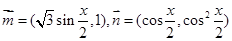 .记
.记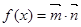
(I)求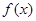 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(Ⅱ)在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为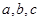 若
若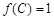 ,
,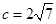 ,
,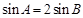 ,求
,求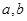 的值.
的值.
已知函数 ,其中常数
,其中常数 .
.
(1)令 ,求函数
,求函数 的单调区间;
的单调区间;
(2)令 ,将函数
,将函数 的图像向左平移
的图像向左平移 个单位,再往上平移
个单位,再往上平移 个单位,得到函数
个单位,得到函数 的图像.对任意的
的图像.对任意的 ,求
,求 在区间
在区间 上零点个数的所有可能值.
上零点个数的所有可能值.
若函数 ,非零向量
,非零向量 ,我们称
,我们称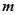 为函数
为函数 的“相伴向量”,
的“相伴向量”, 为向量
为向量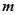 的“相伴函数”.
的“相伴函数”.
(1)已知函数 的最小正周期为
的最小正周期为 ,求函数
,求函数 的“相伴向量”;
的“相伴向量”;
(2)记向量 的“相伴函数”为
的“相伴函数”为 ,将
,将 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移 个单位长度,得到函数
个单位长度,得到函数 ,若
,若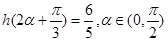 ,求
,求 的值;
的值;
(3)对于函数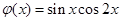 ,是否存在“相伴向量”?若存在,求出
,是否存在“相伴向量”?若存在,求出 “相伴向量”;
“相伴向量”;
若不存在,请说明理由.
给出下列命题:
(1)存在实数 ,使
,使 (2)存在实数
(2)存在实数 ,使
,使
(3)函数 是偶函数 (4)若
是偶函数 (4)若 是第一象限的角,且
是第一象限的角,且 ,则
,则 .其中正确命题的序号是________________________________
.其中正确命题的序号是________________________________