福建省高三高考压轴理科数学试卷
下列命题正确的是( )
A.存在x0∈R,使得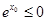 的否定是:不存在x0∈R,使得 的否定是:不存在x0∈R,使得 ; ; |
B.存在x0∈R,使得 的否定是:任意x∈R,均有 的否定是:任意x∈R,均有 |
| C.若x=3,则x2-2x-3=0的否命题是:若x≠3,则x2-2x-3≠0. |
D.若 为假命题,则命题p与q必一真一假 为假命题,则命题p与q必一真一假 |
已知平面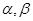 和直线
和直线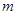 ,给出条件:①
,给出条件:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .为使
.为使 ,应选择下面四个选项中的( )
,应选择下面四个选项中的( )
| A.③⑤ | B.①⑤ | C.①④ | D.②⑤ |
如图,在△ABC中,AB=3,AC=5,若O为△ABC的外心,则 的值是(( )
的值是(( )
A.4 |
B.8 | C.6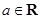 |
D.6 |
如图,设圆弧 与两坐标轴正半轴围成的扇形区域为
与两坐标轴正半轴围成的扇形区域为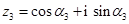 ,过圆弧上一点
,过圆弧上一点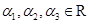 做该圆的切线与两坐标轴正半轴围成的三角形区域为
做该圆的切线与两坐标轴正半轴围成的三角形区域为 .现随机在区域
.现随机在区域 内投一点
内投一点 ,若设点
,若设点 落在
落在
区域 内的概率为
内的概率为 ,则
,则 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |

为调查某校学生喜欢数学课的人数比例,采用如下调查方法:
(1)在该校中随机抽取100名学生,并编号为1,2,3, ,100;
(2)在箱内放置两个白球和三个红球,让抽取的100名学生分别从箱中随机摸出一球,记住其颜色并放回;
(3)请下列两类学生举手:(ⅰ)摸到白球且号数为偶数的学生;(ⅱ)摸到红球且不喜欢数学课的学生.
如果总共有26名学生举手,那么用概率与统计的知识估计,该校学生中喜欢数学课的人数比例大约是( )
| A.88% | B.90% | C.92% | D.94% |
已知 与
与 都是定义在R上的函数,
都是定义在R上的函数, ,且
,且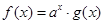
 ,且
,且 ,在有穷数列
,在有穷数列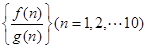 中,任意取前
中,任意取前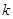 项相加,则前
项相加,则前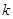 项和大于
项和大于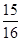 的概率是( )
的概率是( )
A. |
B. |
C.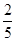 |
D.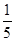 |
已知一个几何体是由上下两部分构成的组合体,其三视图如右图所示,若图中圆的半径为1,等腰三角形的腰长为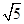 ,则该几何体的体积是 .
,则该几何体的体积是 .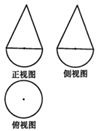
小明在做一道数学题目时发现:若复数
 ,
,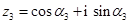 (其中
(其中 ), 则
), 则 ,
,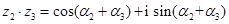 ,根据上面的结论,可以提出猜想: z1·z2·z3= .
,根据上面的结论,可以提出猜想: z1·z2·z3= .
意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数: 1,1,2,3,5,8,13,其中从第三个数起,每一个数都等于他前而两个数的和.该数列是一个非常美丽、和谐的数列,有很多奇妙的属性.比如:随着数列项数的增加,前一项与后一项之比越逼近黄金分割0.6180339887 .人们称该数列{an}为“斐波那契数列”.若把该数列{an}的每一项除以4所得的余数按相对应的顺序组成新数列{bn},在数列{bn}中第2014项的值是_______]
下图是预测到的某地5月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择5月1日至5月13日中的某一天到达该市,并停留2天
(1)求此人到达当日空气质量优良的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明).
已知函数 (
( ,
, ,
, ),
), 的部分图像如图所示,
的部分图像如图所示,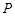 、
、 分别为该图像的最高点和最低点,点
分别为该图像的最高点和最低点,点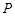 的坐标为
的坐标为 .
.
(1)求 的最小正周期及
的最小正周期及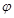 的值;
的值;
(2)若点 的坐标为
的坐标为 ,
,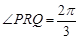 ,求
,求 的值和
的值和 的面积.
的面积.
如图,在圆 上任取一点
上任取一点 ,过点
,过点 作
作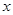 轴的垂线段
轴的垂线段 ,
,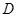 为垂足.设
为垂足.设 为线段
为线段 的中点.
的中点.
(1)当点 在圆
在圆 上运动时,求点
上运动时,求点 的轨迹
的轨迹 的方程;
的方程;
(2)若圆 在点
在点 处的切线与
处的切线与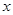 轴交于点
轴交于点 ,试判断直线
,试判断直线 与轨迹
与轨迹 的位置关系.
的位置关系.
如图所示,在边长为 的正方形
的正方形 中,点
中,点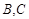 在线段
在线段 上,且
上,且 ,
, ,作
,作 //
//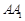 ,分别交
,分别交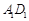 ,
, 于点
于点 ,
,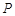 ,作
,作 //
//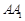 ,分别交
,分别交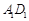 ,
, 于点
于点 ,
, ,将该正方形沿
,将该正方形沿 ,
, 折叠,使得
折叠,使得 与
与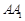 重合,构成如图所示的三棱柱
重合,构成如图所示的三棱柱 .
.
(1)求证: 平面
平面 ;
;
(2)若点E为四边形BCQP内一动点,且二面角E-AP-Q的余弦值为 ,求|BE|的最小值.
,求|BE|的最小值.
设 (
( 是自然对数的底数,
是自然对数的底数, ),且
),且 .
.
(1)求实数 的值,并求函数
的值,并求函数 的单调区间;
的单调区间;
(2)设 ,对任意
,对任意 ,恒有
,恒有 成立.求实数
成立.求实数 的取值范围;
的取值范围;
(3)若正实数 满足
满足 ,
, ,试证明:
,试证明: ;并进一步判断:当正实数
;并进一步判断:当正实数 满足
满足
 ,且
,且 是互不相等的实数时,不等式
是互不相等的实数时,不等式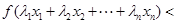
 是否仍然成立.
是否仍然成立.
在直角坐标平面内,将每个点绕原点按逆时针方向旋转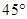 的变换
的变换 所对应的矩阵为
所对应的矩阵为 ,将每个点横、纵坐标分别变为原来的
,将每个点横、纵坐标分别变为原来的 倍的变换
倍的变换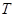 所对应的矩阵为
所对应的矩阵为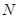 .
.
(1)求矩阵 的逆矩阵
的逆矩阵 ;
;
(2)求曲线 先在变换
先在变换 作用下,然后在变换
作用下,然后在变换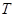 作用下得到的曲线方程.
作用下得到的曲线方程.
在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为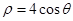 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)分别求出曲线 和直线
和直线 的直角坐标方程;
的直角坐标方程;
(2)若点 在曲线
在曲线 上,且
上,且 到直线
到直线 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点 的个数.
的个数.
 集合
集合 ,
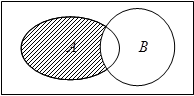
, ,下图中阴影部分所表示的集合为( )
,下图中阴影部分所表示的集合为( )



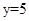 与
与 在区间
在区间 上截曲线
上截曲线 所得的弦长相等且不为零,则下列描述正确的是( )
所得的弦长相等且不为零,则下列描述正确的是( )



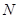 是
是 ,则输出
,则输出 的值是( )
的值是( )
 .若
.若 的二项展开式中
的二项展开式中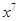 项的系数为-15,则
项的系数为-15,则 _______.
_______.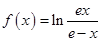 ,则
,则 =_______________。
=_______________。 ,且
,且 .
. 的最小值
的最小值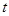 ;
; 满足
满足 ,求证:
,求证: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号