全国普通高等学校招生统一考试文科数学
设四边形的两条对角线为、,则"四边形为菱形"是""的
来源:2014年全国普通高等学校招生统一考试文科数学
为了得到函数 的图象,可以将函数 的图象( )
| A. | 向右平移 个单位长 | B. | 向右平移 个单位长 |
| C. | 向左平移 个单位长 | D. | 向左平移 个单位长 |
来源:2014年全国普通高等学校招生统一考试文科数学
设、是两条不同的直线,、是两个不同的平面,则()
| A. | 若 , ,则 |
| B. | 若 , ,则 |
| C. | 若 , ,则 |
| D. | 若 , , ,则 |
来源:2014年全国普通高等学校招生统一考试文科数学
设为两个非零向量的夹角,已知对任意实数,的最小值为1( )
来源:2014年全国普通高等学校招生统一考试文科数学
如图,某人在垂直于水平地面的墙面前的点处进行射击训练,已知点到墙面的距离为,某目标点沿墙面上的射线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角的大小(仰角为直线与平面所成的角),若,,,则的最大值是( )
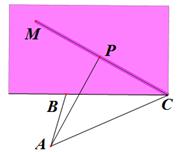
来源:2014年全国普通高等学校招生统一考试文科数学
如图,在四棱锥
中,平面
平面
;
,
.
(1)证明:
平面
;
(2)求直线
与平面
所成的角的正切值.

来源:2014年全国普通高等学校招生统一考试文科数学







 粤公网安备 44130202000953号
粤公网安备 44130202000953号