关于函数f(x)＝4sin(2x＋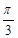
), (x∈R)有下列命题：
①y＝f(x)是以2π为最小正周期的周期函数；
② y＝f(x)可改写为y＝4cos(2x－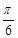
)；
③y＝f(x)的图象关于(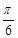－，0)对称；
④ y＝f(x)的图象关于直线x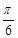＝－对称；
其中正确的序号为 。
中，
，
交
于点
，设
，
，用
表示
______
的图象如图所示，则
；
与
的夹角为
，则
；
的扇形的圆心角为
，则此扇形的面积为；
分别是
的三边
上的高，且满足
，则角
的最大值是.相关知识点
推荐套卷
关于函数f(x)＝4sin(2x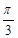＋), (x∈R)有下列命题：
①y＝f(x)是以2π为最小正周期的周期函数；
② y＝f(x)可改写为y＝4cos(2x－)；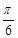
③y＝f(x)的图象关于(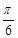－，0)对称；
④ y＝f(x)的图象关于直线x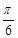＝－对称；
其中正确的序号为 。
粤公网安备 44130202000953号