福建省漳州市普通高中毕业班质量检查理科数学试卷
已知正三棱柱(侧棱与底面垂直,底面是正三角形)的高与底面边长均为1,其直观图 和正(主)视图如图所示,则它的左(侧)视图的面积是 
A. |
B.1 | C. |
D. |
已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是
A.(1- ,2) ,2) |
B.(0,2) | C.( -1,2) -1,2) |
D.(0,1+ ) ) |
已 知F1 ,F2分别是双曲线 的左、右焦点,过F1的直线
的左、右焦点,过F1的直线 与双曲线的左、右两支分别交于A、B两点.若ΔABF2是等边三角形,则该双曲线的离心率为
与双曲线的左、右两支分别交于A、B两点.若ΔABF2是等边三角形,则该双曲线的离心率为
A.2
B.
C.
D.
定义全集U的非空子集P的特征函数 表示集合P在全集U的补集.已知
表示集合P在全集U的补集.已知 均为全集U的非空子集,给出下列命题:
均为全集U的非空子集,给出下列命题:
①若 ,则对于任意
,则对于任意 ;
;
②对于任意 ;
;
③对于任意 ;
;
④对于任意 .
.
则正确命题的序号为
已知向量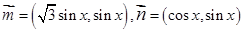 ,函数
,函数 .
.
(1)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)已知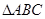 中,角
中,角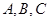 的对边分别为
的对边分别为 ,若
,若 ,
, ,
,
求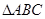 的面积.
的面积.
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福指数不低于9.5分,则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记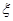 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求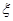 的分布列及数学期望.
的分布列及数学期望.
在四棱锥P-ABCD中,侧面PCD 底面ABCD,PD
底面ABCD,PD CD,底面ABCD是直角梯形,AB∥DC,
CD,底面ABCD是直角梯形,AB∥DC, ,
, ,
, .
.
(1)求证:BC 平面PBD:
平面PBD:
(2)求直线AP与平面PDB所成角的正弦值;
(3)设E为侧棱PC上异于端点的一点, ,试确定
,试确定 的值,使得二面角E-BD-P的余弦值为
的值,使得二面角E-BD-P的余弦值为 .
.
已知抛物线C:y2=2px(p>0)的焦点F和椭圆 的右焦点重合,直线
的右焦点重合,直线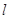 过点F交抛物线于A、B两点.
过点F交抛物线于A、B两点.
(1)求抛物线C的方程;
(2)若直线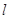 交y轴于点M,且
交y轴于点M,且 ,m、n是实数,对于直线
,m、n是实数,对于直线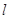 ,m+n是否为定值?
,m+n是否为定值?
若是,求出m+n的值;否则,说明理由.
巳知函数 ,
, ,其中
,其中 .
.
(1)若 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;
(2)若 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(3)记 ,求证:
,求证: .
.
在直角坐标系 中,直线
中,直线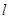 的方程为
的方程为 ,曲线
,曲线 的参数方程为
的参数方程为 .
.
(1)已知在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为
的极坐标为 ,判断点
,判断点 与直线
与直线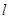 的位置关系;
的位置关系;
(2)设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线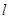 的距离的最小值.
的距离的最小值.
 等于
等于 展开式中的常数项为
展开式中的常数项为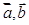 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,则
,则 等于
等于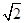

 ,则输出的
,则输出的 的值为
的值为
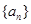 的前
的前 项和为
项和为 ,若
,若 ,则
,则 等于
等于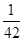
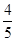


 的定义域为[a,b],值域为[-2,1],则
的定义域为[a,b],值域为[-2,1],则 的值不可能是
的值不可能是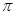



 为
为 上的可导函数,且
上的可导函数,且 ,均有
,均有 ,则以下判断正确的是
,则以下判断正确的是
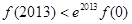

 大小无法确定
大小无法确定 =_________.
=_________. 中,
中, , 数列
, 数列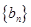 是等比数列,且
是等比数列,且 ,则
,则 的值为 .
的值为 .
 .
. 的逆矩阵
的逆矩阵 ;
; 的特征值
的特征值 、
、 和对应的特征向量
和对应的特征向量 、
、 .
.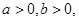 且
且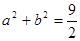 ,若
,若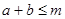 恒成立,
恒成立, 的最小值;(2)若
的最小值;(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号