某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福指数不低于9.5分,则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
推荐套卷
 ,使得直线
,使得直线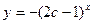 在实数集R上为增函数,命题q:不等式
在实数集R上为增函数,命题q:不等式 在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围.
在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围. (单位:百万元)与销售额
(单位:百万元)与销售额 (单位:百万元)之间有如下对应数据
(单位:百万元)之间有如下对应数据 
 )
) 有共同焦点,且过点
有共同焦点,且过点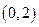 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号