[安徽省“皖西七校”高三年级联合考试文科数学试卷
“ ”是“
”是“ ”的( )
”的( )
| A.充分必要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
来源:2014届安徽省“皖西七校”高三年级联合考试文科数学试卷
已知 是两条不重合的直线,
是两条不重合的直线, 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题:
①若 ,
, ,且
,且 ,则
,则 ;
;
②若 ,
, ,且
,且 ,则
,则 ;
;
③若 ,
, ,且
,且 ,则
,则 ;
;
④若 ,
, ,且
,且 ,则
,则 .
.
其中正确命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
来源:2014届安徽省“皖西七校”高三年级联合考试文科数学试卷
在等比数列 中,
中, 是它的前
是它的前 项和,若
项和,若 ,且
,且 与
与 的等差中项为17,则
的等差中项为17,则 ( )
( )
A. |
B.16 | C.15 | D. |
来源:2014届安徽省“皖西七校”高三年级联合考试文科数学试卷
若直线 上不同的三个点
上不同的三个点 与直线
与直线 外一点
外一点 ,使得
,使得 成立,则满足条件的实数
成立,则满足条件的实数 的集合为( )
的集合为( )
A. |
B. |
C. |
D. |
来源:2014届安徽省“皖西七校”高三年级联合考试文科数学试卷
已知圆 ,定点
,定点 ,点
,点 为圆
为圆 上的动点,点
上的动点,点 在
在 上,点
上,点 在线段
在线段 上,且满足
上,且满足 ,则点
,则点 的轨迹方程是( )
的轨迹方程是( )
A. |
B. |
C. |
D. |
来源:2014届安徽省“皖西七校”高三年级联合考试文科数学试卷
已知圆 ,直线
,直线 ,给出下面四个命题:
,给出下面四个命题:
①对任意实数 和
和 ,直线
,直线 和圆
和圆 有公共点;
有公共点;
②对任意实数 ,必存在实数
,必存在实数 ,使得直线
,使得直线 与和圆
与和圆 相切;
相切;
③对任意实数 ,必存在实数
,必存在实数 ,使得直线
,使得直线 与和圆
与和圆 相切;
相切;
④存在实数 与
与 ,使得圆
,使得圆 上有一点到直线
上有一点到直线 的距离为3.
的距离为3.
其中正确的命题是(写出所有正确命题的序号)
来源:2014届安徽省“皖西七校”高三年级联合考试文科数学试卷
如图,在四棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,平面
,平面 底面
底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
来源:2014届安徽省“皖西七校”高三年级联合考试文科数学试卷
已知函数 .
.
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线 平行,求实数
平行,求实数 的值;
的值;
(2)若函数 在
在 处取得极小值,且
处取得极小值,且 ,求实数
,求实数 的取值范围.
的取值范围.
来源:2014届安徽省“皖西七校”高三年级联合考试文科数学试卷
如图,半径为30 的圆形(
的圆形( 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料 ,其中点
,其中点 在圆弧上,点
在圆弧上,点 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设 与矩形材料的边
与矩形材料的边 的夹角为
的夹角为 ,圆柱的体积为
,圆柱的体积为
 .
.
(1)求 关于
关于 的函数关系式?
的函数关系式?
(2)求圆柱形罐子体积 的最大值.
的最大值.
来源:2014届安徽省“皖西七校”高三年级联合考试文科数学试卷
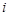 是虚数单位,若复数满足
是虚数单位,若复数满足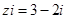 ,则
,则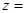 ( )
( )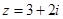
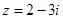
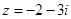
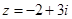
 ,集合
,集合 ,
, ,则
,则 ( )
( )



 满足
满足 ,则
,则 的最小值是( )
的最小值是( )

 ,若关于
,若关于 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是( )
的取值范围是( )



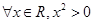 ”的否定是.
”的否定是.
 的单调递减区间是
的单调递减区间是 ,则实数
,则实数 .
. 是夹角为
是夹角为 的单位向量,且
的单位向量,且 ,
, ,则
,则 .
. ,钝角
,钝角 (角
(角 对边为
对边为 )的角
)的角 满足
满足 .
. 的单调递增区间;
的单调递增区间; ,求
,求 .
.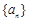 的前
的前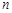 项和为
项和为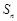 满足
满足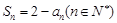 .
.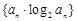 的前
的前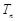 .
. 经过点
经过点 ,其左、右顶点分别是
,其左、右顶点分别是 、
、 ,左、右焦点分别是
,左、右焦点分别是 、
、 ,
, (异于
(异于 交直线
交直线 于
于 、
、 两点,若
两点,若 成等比数列.
成等比数列.
 为直径的圆过点
为直径的圆过点 粤公网安备 44130202000953号
粤公网安备 44130202000953号