高中数学一阶、二阶线性常系数递归数列的通项公式解答题

我们已经学过了等差数列，你是否想到过有没有等和数列呢？
（1）类比“等差数列”给出“等和数列”的定义；
（2）探索等和数列{a_n}的奇数项与偶数项各有什么特点？并加以说明．

已知为锐角，且，函数，数列的首项，.
（1）求函数的表达式；（2）求数列的前项和．

对于数对序列，记，，其中表示和两个数中最大的数.
（1）对于数对序列，求的值；

（2）记为四个数中最小的数，对于由两个数对组成的数对序列和，试分别对和两种情况比较和的大小；（3）在由五个数对组成的所有数对序列中，写出一个数对序列使最小，并写出的值.(只需写出结论).

已知数列满足
（1）若，数列单调递增，求实数的取值范围。
（2）若，试写出对任意成立的充要条件，并证明你的结论。

（本小题满分12分）已知等差数列的前项和为，且，.
（Ⅰ）求数列 的通项；  
（Ⅱ）设，求数列的前n项和.

已知函数f(x)＝的图象过原点，且关于点(－1,2)成中心对称．
(1)求函数f(x)的解析式；
(2)若数列{a_n}满足a₁＝2，a_n＋1＝f(a_n)，试证明数列为等比数列，并求出数列{a_n}的通项公式．

（本小题满分14分）
已知等差数列的公差为,且,数列的前项和为,且
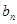
（1）求数列,的通项公式；
（2）记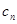= 求证：数列的前项和 。

设同时满足条件：①≤b_n＋1(n∈N^*)；②b_n≤M(n∈N^*，M是与n无关的常数)的无穷数列{b_n}叫“特界” 数列．
(1) 若数列{a_n}为等差数列，S_n是其前n项和，a₃＝4，S₃＝18，求S_n；
(2) 判断(1)中的数列{S_n}是否为“特界” 数列，并说明理由．

（本小题满分13分） 设数列满足;
（1）当时，求并由此猜测的一个通项公式；
（2）当时，证明对所有的，
（i）
（ii）。          

(本题满分12分)本题共有2个小题，第1小题满分5分，第2小题满分7分．
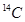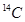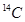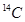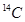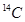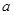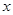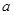　　要测定古物的年代，常用碳的放射性同位素的衰减来测定：在动植物的体内都含有微量的，动植物死亡后，停止了新陈代谢，不再产生，且原有的含量的衰变经过5570年(的半衰期)，它的残余量只有原始量的一半．若的原始含量为，则经过年后的残余量与之间满足．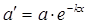
(1) 求实数的值；
(2) 测得湖南长沙马王堆汉墓女尸中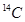的残余量约占原始含量的76.7%，试推算马王堆古墓的年代(精确到100年)．

对于给定数列，如果存在实常数，使得对于任意都成立，我们称数列是 “类数列”．
（Ⅰ）已知数列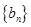是 “类数列”且，求它对应的实常数的值；
（Ⅱ）若数列满足，，求数列的通项公式．并判断是否为“类数列”，说明理由．

下图是一个三角形数阵，从第二行起每个数都等于它肩上两个数的和，第行的第一个数为
（Ⅰ）写出关于的表达式：
，不需证明。
（Ⅱ）求第行中所有数的和；
（Ⅲ）当时，求数阵中所有
数的和．

（本小题满分14分）已知正数数列满足：，其中为数列的前项和．
（1）求数列的通项；
（2）令，求的前n项和T_n..

已知等差数列{a_n}的前n项的和记为S_n．如果a₄＝－12， a₈＝－4．
(1)求数列{a_n}的通项公式；
(2)求S_n的最小值及其相应的n的值；
(3)从数列{a_n}中依次取出a₁，a₂，a₄，a₈，…，，…，构成一个新的数列{b_n}，求{b_n}的前n项和．

（本小题满分12分）已知数列{a_n}满足   a₁＝1,a_n＋1＝.,写出它的前5项,并归纳出数列的一个通项公式(不要求证明)