高中数学一阶、二阶线性常系数递归数列的通项公式解答题

设数列的前n项积为；数列的前n项和为．
（1）设．①证明数列成等差数列；②求证数列的通项公式；
（2）若恒成立，求实数k的取值范围．

有限数列D:,,…,,其中为数列D的前项和，定义为D的“德光和”，若有项的数列,,…,的“德光和”为，则有项的数列8，,,…,的“德光和”为

某市为控制大气PM2.5的浓度，环境部门规定：该市每年的大气主要污染物排放总量不能超过55万吨，否则将采取紧急限排措施.已知该市2013年的大气主要污染物排放总量为40万吨，通过技术改造和倡导绿色低碳生活等措施，此后每年的原大气主要污染物排放最比上一年的排放总量减少10%.同时，因为经济发展和人口增加等因素，每年又新增加大气主要污染物排放量万吨.
（1）从2014年起，该市每年大气主要污染物排放总量（万吨）依次构成数列，求相邻两年主要污染物排放总量的关系式；
（2）证明：数列是等比数列；
（3）若该市始终不需要采取紧急限排措施，求m的取值范围.

数列{a_n}的前n项和记为S_n，已知a₁＝1，a_n＋1＝S_n(n＝1，2，3，…)，证明：
(1)数列是等比数列；
(2)S_n＋1＝4a_n.

本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．
从数列中取出部分项，并将它们按原来的顺序组成一个数列，称之为数列的一个子数列．
设数列是一个首项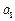为、公差为的无穷等差数列．
（1）若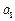，，成等比数列，求其公比．
（2）若，从数列中取出第2项、第6项作为一个等比数列的第1项、第2项，试问该数列是否为的无穷等比子数列，请说明理由．
（3）若，从数列中取出第1项、第项（设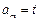）作为一个等比数列的第1项、第2项．求证：当为大于1的正整数时，该数列为的无穷等比子数列．

已知数列{a_n}的前n项和是S_n，且S_n＋a_n＝1.
(1)求数列{a_n}的通项公式；
(2)记b_n＝log₃，数列的前n项和为T_n，证明：T_n<.

已知（）是曲线上的点，，是数列的前项和，且满足，， ．
（1）证明：数列（）是常数数列；
（2）确定的取值集合，使时，数列是单调递增数列；
（3）证明：当时，弦（）的斜率随单调递增

已知数列{a_n}满足：a₁＝，a_n＋1＝ (n∈N^*)．
(1)求a₂，a₃的值；
(2)证明：不等式0＜a_n＜a_n＋1对于任意n∈N^*都成立．

（本小题满分13分）
对于各项均为整数的数列，如果(=1，2，3，…)为完全平方数，则称数
列具有“性质”。
不论数列是否具有“性质”，如果存在与不是同一数列的，且同
时满足下面两个条件：①是的一个排列；②数列具有“性质”，则称数列具有“变换性质”。
（I）设数列的前项和，证明数列具有“性质”；
（II）试判断数列1，2，3，4，5和数列1，2，3，…，11是否具有“变换性质”，具有此性质的数列请写出相应的数列，不具此性质的说明理由；
（III）对于有限项数列：1，2，3，…，，某人已经验证当时，
数列具有“变换性质”，试证明：当”时，数列也具有“变换性质”。

（本小题满分12分）
设数列为等差数列，且，，数列的前项和为，
（Ⅰ）求数列的通项公式；
（Ⅱ）若，求数列的前项和.

已知二次函数f(x)=px²+qx(p≠0),其导函数为f'(x)=6x-2,数列{a_n}的前n项和为S_n,点(n,S_n)(n∈N^*)均在函数y=f(x)的图象上.
(1)求数列{a_n}的通项公式.
(2)若c_n=(a_n+2),2b₁+2²b₂+2³b₃+…+2ⁿb_n=c_n,求数列{b_n}的通项公式.

已知函数f（x）=x²－ax+b（a，b∈R）的图像经过坐标原点，且，数列{}的前n项和=f（n）（n∈N^*）.
（Ⅰ）求数列{}的通项公式；
（Ⅱ）若数列{}满足+ = ,求数列{}的前n项和.

已知数列{a_n}的前n项和为S_n，且满足S_n＝n²，数列{b_n}满足b_n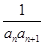＝，T_n为数列{b_n}的前n项和．
(1)求数列{a_n}的通项公式a_n和T_n；
(2)若对任意的n∈N^*，不等式λT_n<n＋(－1)ⁿ恒成立，求实数λ的取值范围．

我们已经学过了等差数列，你是否想到过有没有等和数列呢？
（1）类比“等差数列”给出“等和数列”的定义；
（2）探索等和数列{a_n}的奇数项与偶数项各有什么特点？并加以说明．

已知为锐角，且，函数，数列的首项，.
（1）求函数的表达式；（2）求数列的前项和．