本题共有3个小题,第1小题满分4分,第2小题满分6分,
第3小题满分8分.
如果数列 同时满足:(1)各项均为正数,(2)存在常数k, 对任意
同时满足:(1)各项均为正数,(2)存在常数k, 对任意 都成立,那么,这样的数列
都成立,那么,这样的数列 我们称之为“类等比数列” .由此各项均为正数的等比数列必定是“类等比数列” .问:
我们称之为“类等比数列” .由此各项均为正数的等比数列必定是“类等比数列” .问:
(1)若数列 为“类等比数列”,且k=(a2-a1)2,求证:a1、a2、a3成等差数列;
为“类等比数列”,且k=(a2-a1)2,求证:a1、a2、a3成等差数列;
(2)若数列 为“类等比数列”,且k=
为“类等比数列”,且k= , a2、a4、a5成等差数列,求的值;
, a2、a4、a5成等差数列,求的值;
(3)若数列 为“类等比数列”,且a1=a,a2=b(a、b为常数),是否存在常数λ,使得
为“类等比数列”,且a1=a,a2=b(a、b为常数),是否存在常数λ,使得 对任意
对任意 都成立?若存在,求出λ;若不存在,说明理由.
都成立?若存在,求出λ;若不存在,说明理由.
已知数列 和
和 满足:
满足: ,其中
,其中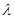 为实数,
为实数, 为正整数.
为正整数.
(1)对任意实数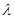 ,求证:
,求证: 不成等比数列;
不成等比数列;
(2)试判断数列 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.
(3)设 为数列
为数列 的前
的前 项和.是否存在实数
项和.是否存在实数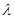 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有 ?若存在,求
?若存在,求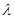 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
已知数列{an}中,a1=2,n∈N*,an>0,数列{an}的前n项和为Sn,且满足an+1= .
.
(1)求{Sn}的通项公式;
(2)设{bk}是{Sn}中的按从小到大顺序组成的整数数列.
①求b3;
②存在N(N∈N*),当n≤N时,使得在{Sn}中,数列{bk}有且只有20项,求N的范围.
已知数列{an}满足a1=a(a>0,a∈N*),a1+a2+…+an-pan+1=0(p≠0,p≠-1,n∈N*).
(1)求数列{an}的通项公式an;
(2)若对每一个正整数k,若将ak+1,ak+2,ak+3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为dk.①求p的值及对应的数列{dk}.
②记Sk为数列{dk}的前k项和,问是否存在a,使得Sk<30对任意正整数k恒成立?若存在,求出a的最大值;若不存在,请说明理由.
已知数列 满足
满足 ,
, ,(
,( )
)
(1)若 ,数列
,数列 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;
(2)若 ,试写出
,试写出 对任意
对任意 成立的充要条件,并证明你的结论.
成立的充要条件,并证明你的结论.
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知 ,且
,且 ,
, ,数列
,数列 、
、 满足
满足 ,
, ,
, ,
, .
.
(1) 求证数列 是等比数列;
是等比数列;
(2) (理科)求数列 的通项公式
的通项公式 ;
;
(3) (理科)若 满足
满足 ,
, ,
, ,试用数学归纳法证明:
,试用数学归纳法证明: .
.
(本小题满分13分)
若有穷数列 ,
, ,
, (
( 是正整数)满足条件:
是正整数)满足条件: ,则称其为“对称数列”.例如,
,则称其为“对称数列”.例如, 和
和 都是“对称数列”.
都是“对称数列”.
(Ⅰ)若 是25项的“对称数列”,且
是25项的“对称数列”,且

 ,
, 是首项为1,公比为2的等比数列.求
是首项为1,公比为2的等比数列.求 的所有项和
的所有项和 ;
;
(Ⅱ)若 是50项的“对称数列”,且
是50项的“对称数列”,且

 ,
, 是首项为1,公差为2的等差数列.求
是首项为1,公差为2的等差数列.求 的前
的前 项和
项和 ,
, .
.
已知数列 的前
的前 项和为
项和为 满足
满足 .
.
(1)函数 与函数
与函数 互为反函数,令
互为反函数,令 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(2)已知数列 满足
满足 ,证明:对任意的整数
,证明:对任意的整数 ,有
,有 .
.
在数列 中,
中, .从数列
.从数列 中选出
中选出 项并按原顺序组成的新数列记为
项并按原顺序组成的新数列记为 ,并称
,并称 为数列
为数列 的
的 项子列.例如数列
项子列.例如数列 、
、 、
、 、
、 为
为 的一个
的一个 项子列.
项子列.
(1)试写出数列 的一个
的一个 项子列,并使其为等差数列;
项子列,并使其为等差数列;
(2)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等差数列,证明:
为等差数列,证明: 的公差
的公差 满足
满足 ;
;
(3)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等比数列,证明:
为等比数列,证明:
 .
.
设各项都是正整数的无穷数列 满足:对任意
满足:对任意 ,有
,有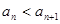 .记
.记 .
.
(1)若数列 是首项
是首项 ,公比
,公比 的等比数列,求数列
的等比数列,求数列 的通项公式;
的通项公式;
(2)若 ,证明:
,证明: ;
;
(3)若数列 的首项
的首项 ,
, ,
, 是公差为1的等差数列.记
是公差为1的等差数列.记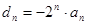 ,
, ,问:使
,问:使 成立的最小正整数
成立的最小正整数 是否存在?并说明理由.
是否存在?并说明理由.
已知数列 的前
的前 项和为
项和为 ,
, ,且
,且 (
( 为正整数)
为正整数)
(1)求数列 的通项公式;
的通项公式;
(2)对任意正整数 ,是否存在
,是否存在 ,使得
,使得 恒成立?若存在,求是实数
恒成立?若存在,求是实数 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
设 是给定的正整数,有序数组(
是给定的正整数,有序数组( )中
)中 或
或
 .
.
(1)求满足“对任意的 ,
, ,都有
,都有 ”的有序数组(
”的有序数组( )的个数
)的个数 ;
;
(2)若对任意的 ,
, ,
, ,都有
,都有 成立,求满足“存在
成立,求满足“存在 ,使得
,使得 ”的有序数组(
”的有序数组( )的个数
)的个数
对于给定数列 ,如果存在实常数
,如果存在实常数 使得
使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “线性数列”.
是 “线性数列”.
(1)若 ,
, ,
, ,数列
,数列 、
、 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列 是“线性数列”,则数列
是“线性数列”,则数列 也是“线性数列”;
也是“线性数列”;
(3)若数列 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列 前
前 项的和.
项的和.