(本小题满分16分)已知数列 、
、 满足
满足 ,
, ,其中
,其中 ,则称
,则称 为
为 的“生成数列”.
的“生成数列”.
(1)若数列 的“生成数列”是
的“生成数列”是 ,求
,求 ;
;
(2)若 为偶数,且
为偶数,且 的“生成数列”是
的“生成数列”是 ,证明:
,证明: 的“生成数列”是
的“生成数列”是 ;
;
(3)若 为奇数,且
为奇数,且 的“生成数列”是
的“生成数列”是 ,
, 的“生成数列”是
的“生成数列”是 ,…,依次将数列
,…,依次将数列 ,
, ,
, ,…的第
,…的第 项取出,构成数列
项取出,构成数列 .
.
探究:数列 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.
已知等差数列{an}的前n项的和记为Sn.如果a4=-12, a8=-4.
(1)求数列{an}的通项公式;
(2)求Sn的最小值及其相应的n的值;
(3)从数列{an}中依次取出a1,a2,a4,a8,…, ,…,构成一个新的数列{bn},求{bn}的前n项和.
,…,构成一个新的数列{bn},求{bn}的前n项和.
(本小题满分12分)已知数列 的前
的前 项和是
项和是 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设
 ,求适合方程
,求适合方程 的
的 的值.
的值.
(Ⅲ)记 ,是否存在实数M,使得对一切
,是否存在实数M,使得对一切 恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
恒成立,若存在,请求出M的最小值;若不存在,请说明理由。
下图是一个三角形数阵 ,从第二行起每个数都等于它肩上两个数的和,第
,从第二行起每个数都等于它肩上两个数的和,第 行的第一个数为
行的第一个数为
(Ⅰ)写出 关于
关于 的表达式:
的表达式: ,不需证明。
,不需证明。
(Ⅱ)求第 行中所有数的和
行中所有数的和 ;
;
(Ⅲ)当 时,求数阵中所有
时,求数阵中所有
数的和 .
.
(本小题满分14分)
已知等差数列 的公差为
的公差为 ,且
,且 ,数列
,数列 的前
的前 项和为
项和为 ,且
,且

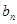


(1)求数列 ,
, 的通项公式;
的通项公式;
(2)记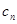 =
= 求证:数列
求证:数列 的前
的前 项和
项和  。
。
已知数列{an}满足a1=1,an=3n-1+an-1(n≥2).
(1)求a2,a3.(2)求通项公式an.
已知数列{an}中,a1=1,前n项和为Sn且Sn+1= Sn+1,n∈N*.
Sn+1,n∈N*.
(1)求数列{an}的通项公式.
(2)求数列{ }的前n项和Tn.
}的前n项和Tn.
(本小题满分14分)设等差数列 的前
的前 项和为
项和为 且
且 .
.
(1)求数列 的通项公式及前
的通项公式及前 项和公式;
项和公式;
(2)设数列 的通项公式为
的通项公式为 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得
 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
已知数列{an}满足前n项和Sn=n2+1,数列{bn}满足bn= ,且前n项和为Tn,设cn=T2n+1-Tn.
,且前n项和为Tn,设cn=T2n+1-Tn.
(1)求数列{bn}的通项公式.
(2)判断数列{cn}的增减性.