下图是一个三角形数阵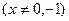
，从第二行起每个数都等于它肩上两个数的和，第
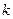行的第一个数为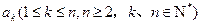
（Ⅰ）写出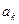
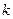关于的表达式：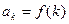
，不需证明。
（Ⅱ）求第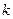行中所有数的和
；
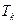（Ⅲ）当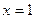
时，求数阵中所有
数的和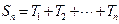
．
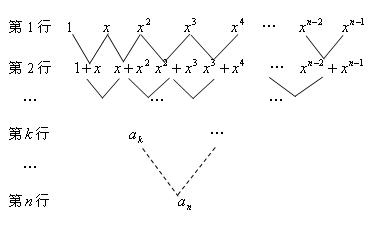
相关试题
，且
,
,试证：
。
是方程
的两个根，求实数
和
的值.相关知识点
推荐套卷
下图是一个三角形数阵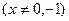，从第二行起每个数都等于它肩上两个数的和，第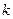行的第一个数为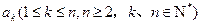
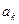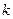（Ⅰ）写出关于的表达式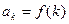：，不需证明。
（Ⅱ）求第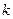行中所有数的和；
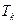（Ⅲ）当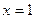时，求数阵中所有
数的和．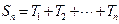
粤公网安备 44130202000953号