高中数学一阶、二阶线性常系数递归数列的通项公式填空题

如图是见证魔术师“论证”64＝65飞神奇．对这个乍看起来颇为神秘的现象，我们运用数学知识不难发现其中的谬误．另外，我们可以更换图中的数据，就能构造出许多更加直观与“令人信服”的“论证”．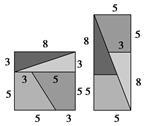

请你用数列知识归纳：(1)这些图中的数所构成的数列：________；(2)写出与这个魔术关联的一个数列递推关系式：________.

数列中,,若存在实数,使得数列为
等差数列,则=_________.

对任意x∈R,函数f(x)满足f(x+1)= + ,设a_n=[f(n)]²-f(n),数列{a_n}的前15项的和为,则f(15)=　　　　.

已知数列满足，给出下列命题：
①当时，数列为递减数列
②当时，数列不一定有最大项
③当时，数列为递减数列
④当为正整数时，数列必有两项相等的最大项
请写出正确的命题的序号____

如图，互不相同的点A₁，A₂，…，A_n，…和B₁，B₂，…，B_n，…分别在角O的两条边上，所有A_nB_n相互平行，且所有梯形A_nB_nB_n＋1A_n＋1的面积均相等，设OA_n＝a_n.若a₁＝1，a₂＝2，则数列{a_n}的通项公式是________．

对于数列{a_n}，定义数列{a_n＋1－a_n}为数列{a_n}的“差数列”，若a₁＝2，{a_n}的“差数列”的通项为2ⁿ，则数列{a_n}的前n项和S_n＝________.

已知数列的通项公式为，数列的通项公式为，
设若在数列中，对任意恒成立，则实数的取值范围是                      ．

设关于x的不等式x²－x＜2nx(n∈N^*)的解集中整数的个数为a_n，数列{a_n}的前n项和为S_n，则的值为________．

数列中,,(是常数,),且成公比不为的等比数列,则的通项公式是______.

已知数列满足，给出下列命题：
①当时，数列为递减数列
②当时，数列不一定有最大项
③当时，数列为递减数列
④当为正整数时，数列必有两项相等的最大项
请写出正确的命题的序号____

在一个数列中，如果对任意,都有为常数，那么这个数列叫做等积数列，叫做这个数列的公积．已知数列是等积数列，且，公积为，记的前项和为，则：
（1）          ．
（2）           ．

设S_n为数列{a_n}的前n项和，若 (n∈N^*)是非零常数，则称该数列为“和等比数列”；若数列{c_n}是首项为2，公差为d(d≠0)的等差数列，且数列{c_n}是“和等比数列”，则d＝________.

如果存在常数a使得数列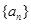满足：若x是数列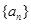中的任意一项，则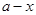也是数列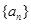中的一项，称数列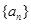为“兑换数列”，常数a是它的“兑换系数”．如数列：1，3，6，8是以9为“兑换系数”的“兑换数列”．已知等差数列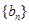是“兑换数列”，则数列的“兑换系数”是         ．

已知，定义.
（1）如果，则       ；
（2）如果，则的取值范围是               .

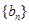在轴的正方向上，从左向右依次取点列 ，以及在第一象限内的抛物线上从左向右依次取点列，使（）都是等边三角形，其中是坐标原点，则第2005个等边三角形的边长是      ．