上海市虹口区高三5月模拟考试文科数学试卷
一个口袋内有4个不同的红球,6个不同的白球,若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7分的取法有多少种 .
来源:2014届上海市虹口区高三5月模拟考试文科数学试卷
已知 、
、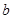 、
、 是
是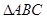 的三边长,且满足
的三边长,且满足 ,则
,则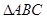 一定是( ).
一定是( ).
| A.等腰非等边三角形 | B.等边三角形 |
| C.直角三角形 | D.等腰直角三角形 |
来源:2014届上海市虹口区高三5月模拟考试文科数学试卷
“ ”是“函数
”是“函数 (
( )在区间
)在区间 上为增函数”的( )
上为增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
来源:2014届上海市虹口区高三5月模拟考试文科数学试卷
如果函数 在
在 上的最大值和最小值分别为
上的最大值和最小值分别为 、
、 ,那么
,那么 .根据这一结论求出
.根据这一结论求出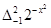 的取值范围( ).
的取值范围( ).
A.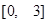 |
B.  |
C. |
D.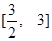 |
来源:2014届上海市虹口区高三5月模拟考试文科数学试卷
如图,直四棱柱 底面
底面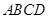 直角梯形,
直角梯形, ∥
∥ ,
,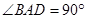 ,
, 是棱
是棱 上一点,
上一点, ,
, ,
, ,
, ,
, .
.
(1)求直四棱柱 的侧面积和体积;
的侧面积和体积;
(2)求证: 平面
平面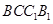 .
.
来源:2014届上海市虹口区高三5月模拟考试文科数学试卷
已知椭圆 ,
, 、
、 是椭圆的左右焦点,且椭圆经过点
是椭圆的左右焦点,且椭圆经过点 .
.
(1)求该椭圆方程;
(2)过点 且倾斜角等于
且倾斜角等于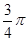 的直线
的直线 ,交椭圆于
,交椭圆于 、
、 两点,求
两点,求 的面积.
的面积.
来源:2014届上海市虹口区高三5月模拟考试文科数学试卷
如图, 、
、 是两个小区所在地,
是两个小区所在地, 、
、 到一条公路
到一条公路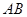 的垂直距离分别为
的垂直距离分别为
 ,
,
 ,
,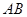 两端之间的距离为
两端之间的距离为
 .
.
(1)某移动公司将在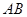 之间找一点
之间找一点 ,在
,在 处建造一个信号塔,使得
处建造一个信号塔,使得 对
对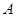 、
、 的张角与
的张角与 对
对 、
、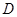 的张角相等,试确定点
的张角相等,试确定点 的位置.
的位置.
(2)环保部门将在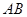 之间找一点
之间找一点 ,在
,在 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得 对
对 、
、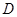 所张角最大,试确定点
所张角最大,试确定点 的位置.
的位置.
来源:2014届上海市虹口区高三5月模拟考试文科数学试卷
阅读:
已知 、
、 ,
, ,求
,求 的最小值.
的最小值.
解法如下: ,
,
当且仅当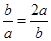 ,即
,即 时取到等号,
时取到等号,
则 的最小值为
的最小值为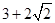 .
.
应用上述解法,求解下列问题:
(1)已知 ,
, ,求
,求 的最小值;
的最小值;
(2)已知 ,求函数
,求函数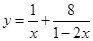 的最小值;
的最小值;
(3)已知正数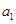 、
、 、
、 ,
, ,
,
求证: .
.
来源:2014届上海市虹口区高三5月模拟考试文科数学试卷
 是第二象限角,则
是第二象限角,则 是第 象限角.
是第 象限角. 满足
满足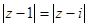 ,则此复数
,则此复数 ,集合
,集合 ,
, ,
,  ,则实数
,则实数 的值为 .
的值为 .
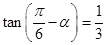 ,则
,则 的值为 .
的值为 . 上的奇函数
上的奇函数 ,
, ,且当
,且当 时,
时,  (
( 为常数),则
为常数),则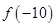 的值为 .
的值为 . 中,
中,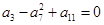 ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则 等于 .
等于 . 、
、 满足约束条件
满足约束条件 ,则
,则 的最小值是 .
的最小值是 .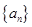 的通项公式为
的通项公式为 ,则
,则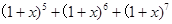 的展开式中
的展开式中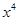 项的系数是数列
项的系数是数列 为实数,若复数
为实数,若复数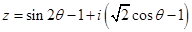 是纯虚数,则
是纯虚数,则 的虚部为 .
的虚部为 . 及其内部一动点
及其内部一动点 ,集合
,集合 ,则集合
,则集合 构成的几何体表面积为 .
构成的几何体表面积为 . 是双曲线
是双曲线 的右支上一点,
的右支上一点, 、
、 分别是圆
分别是圆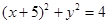 和
和 上的点,则
上的点,则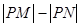 的最大值等于 .
的最大值等于 .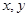 为实数,且满足:
为实数,且满足: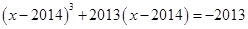 ,
, ,则
,则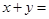 .
. ,
, ,如果
,如果 ∥
∥ ,则实数
,则实数 的值等于( )
的值等于( )



 和
和 满足:
满足: ,其中
,其中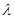 为实数,
为实数, 为正整数.
为正整数. 不成等比数列;
不成等比数列; 为数列
为数列 ?若存在,求
?若存在,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号