2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷
公比为2的等比数列{an}的各项都是正数,且a3a11=16,则a5=( ).
| A.1 | B.2 | C.4 | D.8 |
若{an}为等差数列,Sn是其前n项的和,且S11= π,则tan a6=( ).
π,则tan a6=( ).
A. |
B.- |
C.± |
D.- |
在等差数列{an}中,a8= a11+6,则数列{an}前9项的和S9等于( ).
a11+6,则数列{an}前9项的和S9等于( ).
| A.24 | B.48 | C.72 | D.108 |
设{an}是公差不为0的等差数列,a1=2且a1,a3,a6成等比数列,则{an} 的前n项和Sn=( ).
A. |
B. |
C. |
D.n2+n |
若-9,a,-1成等差数列,-9,m,b,n,-1成等比数列,则ab=( ).
| A.15 | B.-15 | C.±15 | D.10 |
已知实数a,b,c,d成等比数列,且函数y=ln(x+2)-x,当x=b时取到极大值c,则ad等于( ).
| A.1 | B.0 | C.-1 | D.2 |
Sn是等比数列{an}的前n项和,a1= ,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为( ).
,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为( ).
| A.3 | B.4 | C.5 | D.6 |
已知数列{an}的通项公式是an=-n2+12n-32,其前n项和是Sn,对任意的m,n∈N*且m<n,则Sn-Sm的最大值是( ).
| A.-21 | B.4 | C.8 | D.10 |
设公比为q(q>0)的等比数列{an}的前n项和为Sn,若S2=3a2+2,S4=3a4+2,则q=________.
等差数列{an}前9项的和等于前4项的和.若a1=1,ak+a4=0,则k=________.
设y=f(x)是一次函数,f(0)=1,且f(1),f(4),f(13)成等比数列,则f(2)+f(4)+…+f(2n)=________.
已知数列{an}是公差不为0的等差数列,{bn}是等比数列,其中a1=3,b1=1,a2=b2,3a5=b3,若存在常数u,v对任意正整数n都有an=3logubn+v,则u+v=________.
已知数列{an}和{bn}满足:a1=λ,an+1= an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
(1)对任意实数λ,证明:数列{an}不是等比数列;
(2)试判断数列{bn}是否为等比数列,并证明你的结论.
已知数列{an}的前n项和是Sn,且Sn+ an=1.
an=1.
(1)求数列{an}的通项公式;
(2)记bn=log3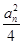 ,数列
,数列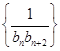 的前n项和为Tn,证明:Tn<
的前n项和为Tn,证明:Tn< .
.
已知等差数列{an}满足:a2=5,a4+a6=22,数列{bn}满足b1+2b2+…
+2n-1bn=nan,设数列{bn}的前n项和为Sn.
(1)求数列{an},{bn}的通项公式;
(2)求满足13<Sn<14的n的集合.
已知函数f(x)=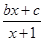 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列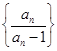 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.
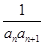 ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和. 粤公网安备 44130202000953号
粤公网安备 44130202000953号