高考数学总复习考点引领+技巧点拨第七章第1课时练习卷
观察下列等式: +2=4;
+2=4; ×2=4;
×2=4; +3=
+3= ;
; ×3=
×3= ;
; +4=
+4= ;
; ×4=
×4= ;…,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________.
;…,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________.
在各项为正的数列{an}中,数列的前n项和Sn满足Sn=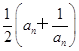 .
.
(1) 求a1,a2,a3;
(2) 由(1)猜想数列{an}的通项公式;
(3) 求Sn.
已知数列{an}满足a1=2,an+1= (n∈N*),则a3=________,a1·a2·a3·…·a2007=________.
(n∈N*),则a3=________,a1·a2·a3·…·a2007=________.
现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 .类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为________.
.类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为________.
已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P为椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线 =1写出具有类似特性的性质,并加以证明.
=1写出具有类似特性的性质,并加以证明.
设同时满足条件:① ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
(1) 若数列{an}为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn;
(2) 判断(1)中的数列{Sn}是否为“特界” 数列,并说明理由.
设数列 满足a1=0且
满足a1=0且 -
- = 1.
= 1.
(1) 求 的通项公式;
的通项公式;
(2) 设bn= ,记Sn=
,记Sn= ,证明:Sn<1.
,证明:Sn<1.
观察下列各式:a+b=1;a2+b2=3;a3+b3=4;a4+b4=7;a5+b5=11;…;则a10+b10=________.
在平面上,若两个正三角形的边长的比为1∶2,则它们的面积比为1∶4,类似地,在空间内,若两个正四面体的棱长的比为1∶2,则它们的体积比为________.
在平面几何里可以得出正确结论:“正三角形的内切圆半径等于这正三角形的高的 ”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号