已知函数 是定义域为
是定义域为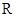 的偶函数. 当
的偶函数. 当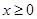 时,
时,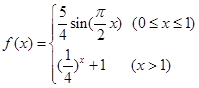 若关于
若关于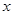 的方程
的方程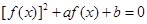 (
(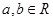 ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数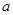 的取值范围是( )
的取值范围是( )
A.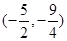 |
B.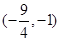 |
C.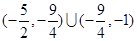 |
D.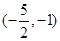 |
已知函数 .
.
(Ⅰ)若 不等式
不等式 的解集为
的解集为 ,
, ,求
,求 的取值范围;
的取值范围;
(Ⅱ)若 为整数,
为整数, ,且函数
,且函数 在
在 上恰有一个零点,求
上恰有一个零点,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,若函数 对任意的x∈
对任意的x∈ ,有
,有 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
已知函数f(x)=-x2+2ex+m-1,g(x)=x+ (x>0).
(x>0).
(1)若g(x)=m有实数根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
已知 (
( )
)
(1)若方程 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得
,使得 在
在 上恰有两个极值点
上恰有两个极值点 ,且满足
,且满足 ,若存在,求实数
,若存在,求实数 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知函数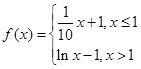 ,则方程
,则方程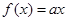 恰有两个不同实数根时,实数
恰有两个不同实数根时,实数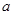 的取值范围是( )
的取值范围是( )
A.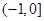 |
B.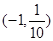 |
C.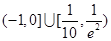 |
D.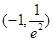 |
已知函数 ,
, .
.
(1)若 ,判断函数
,判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若存在实数 使得关于
使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数 的取值范围.
的取值范围.
定义:对于函数 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数 ,试判断
,试判断 是否为定义域
是否为定义域 上的“局部奇函数”?若是,求出满足
上的“局部奇函数”?若是,求出满足 的
的 的值;若不是,请说明理由;
的值;若不是,请说明理由;
(2)若 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;
(3)若 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
若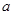 、
、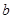 是方程
是方程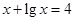 ,
,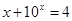 的解,函数
的解,函数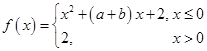 ,则关于
,则关于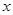 的方程
的方程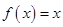 的解的个数是( )
的解的个数是( )
A.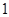 |
B. |
C.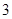 |
D.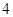 |
若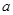 、
、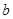 是方程
是方程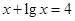 ,
,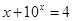 的解,函数
的解,函数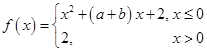 ,则关于
,则关于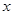 的方程
的方程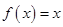 的解的个数是( )
的解的个数是( )
A. |
B. |
C.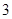 |
D. |