偶函数f(x)满足f(x-1)=f(x+1),且在x∈[0,1]时,f(x)=x,则关于x的方程f(x)= x在x∈[0,4]上解的个数是________.
x在x∈[0,4]上解的个数是________.
已知函数f(x)= ,若存在实数a,b,c,d,满足f(a)=f(b)=f(c)=f(d),其中0<a<b<c<d,则abcd的取值范围 .
,若存在实数a,b,c,d,满足f(a)=f(b)=f(c)=f(d),其中0<a<b<c<d,则abcd的取值范围 .
已知函数f(x)的定义域为R,且f(x)= ,若方程f(x)=x+a有两个不同实根,则a的取值范围为________.
,若方程f(x)=x+a有两个不同实根,则a的取值范围为________.
已知函数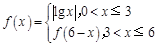 ,设方程
,设方程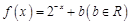 的四个实根从小到大依次为
的四个实根从小到大依次为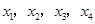 ,对于满足条件的任意一组实根,下列判断中一定正确的为( )
,对于满足条件的任意一组实根,下列判断中一定正确的为( )
A.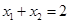 |
B.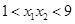 |
C. |
D.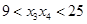 |
已知 (
( )
)
(1)若方程 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得
,使得 在
在 上恰有两个极值点
上恰有两个极值点 ,且满足
,且满足 ,若存在,求实数
,若存在,求实数 的值,若不存在,说明理由.
的值,若不存在,说明理由.
设函数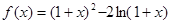
(1)若关于 的不等式
的不等式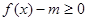 在
在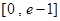 有实数解,求实数
有实数解,求实数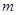 的取值范围;
的取值范围;
(2)设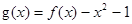 ,若关于
,若关于 的方程
的方程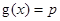 至少有一个解,求
至少有一个解,求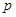 的最小值.
的最小值.
(3)证明不等式: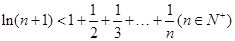
已知函数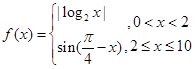 ,若存在实数
,若存在实数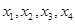 ,且
,且 则
则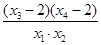 的取值范围是( )
的取值范围是( )
| A.(0,12) | B.(4.16) | C.(9,21) | D.(15,25) |
【原创】已知函数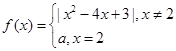 ,若方程
,若方程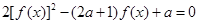 有9个不同的实数解,则实数
有9个不同的实数解,则实数 的取值范围是( )
的取值范围是( )
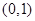 B.
B.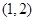 C.
C.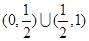 D.
D.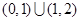
【改编】函数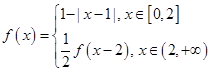 ,则下列命题中正确命题的个数是 ( ).
,则下列命题中正确命题的个数是 ( ).
①函数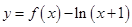 有
有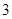 个零点;
个零点;
②若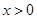 时,函数
时,函数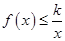 恒成立,则实数
恒成立,则实数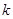 的取值范围是
的取值范围是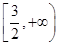 ;
;
③函数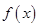 的极大值中一定存在最小值;
的极大值中一定存在最小值;
④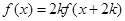
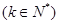 ,对一切
,对一切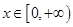 恒成立.
恒成立.
A.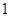 |
B.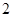 |
C.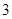 |
D.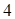 |