已知函数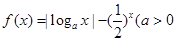 且
且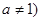 有两个零点
有两个零点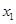 、
、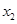 ,则有( )
,则有( )
A.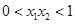 |
B.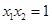 |
C.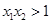 |
D.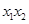 的范围不确定 的范围不确定 |
(本小题满分10分)对于给定的函数 ,定义
,定义 如下:
如下: ,其中
,其中 .
.
(1)当 时,求证:
时,求证: ;
;
(2)当 时,比较
时,比较 与
与 的大小;
的大小;
(3)当 时,求
时,求 的不为0的零点.
的不为0的零点.
已知函数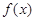 满足
满足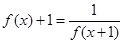 ,当
,当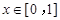 时,
时,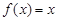 ,若在区间
,若在区间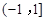 上方程
上方程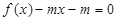 有两个不同的实根,则实数
有两个不同的实根,则实数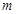 的取值范围是( )
的取值范围是( )
A.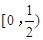 |
B.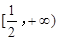 |
C.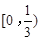 |
D.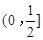 |
已知函数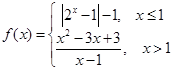 ,下列关于函数
,下列关于函数 (其中a为常数)的叙述中:
(其中a为常数)的叙述中:
①对 a∈R,函数g(x)至少有一个零点;
a∈R,函数g(x)至少有一个零点;
②当a=0时,函数g(x)有两个不同零点;
③ a∈R,使得函数g(x)有三个不同零点;
a∈R,使得函数g(x)有三个不同零点;
④函数g(x)有四个不同零点的充要条件是a<0.
其中真命题有________.(把你认为的真命题的序号都填上)
(本题满分18分)本题共3小题,第(1)小题6分,第(2)小题6分,第(3)小题6分.
已知函数 .
. 
(1)指出 的基本性质(结论不要求证明)并作出函数
的基本性质(结论不要求证明)并作出函数 的图像;
的图像;
(2)关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)关于 的方程
的方程 (
( )恰有6个不同的实数解,求
)恰有6个不同的实数解,求 的取值范围.
的取值范围.
已知 ,函数
,函数 的零点从小到大依次为
的零点从小到大依次为 ,
, .
.
(Ⅰ)若 (
( ),试写出所有的
),试写出所有的 值;
值;
(Ⅱ)若 ,
, ,
, ,求证:
,求证:  ;
;
(Ⅲ)若 ,
, ,
, ,试把数列
,试把数列 的前
的前 项及
项及 按从小到大的顺序排列。(只要求写出结果).
按从小到大的顺序排列。(只要求写出结果).
已知函数 在
在 上有最大值1和最小值0,设
上有最大值1和最小值0,设 (
(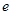
为自然对数的底数).
(1)求 的值;
的值;
(2)若不等式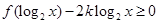 在
在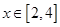 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若方程 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
己知函数
(1)若 是
是 的极值点,求
的极值点,求 在
在 上的最大值;
上的最大值;
(2)在(1)的条件下,是否存在实数b,使得函数 的图象与函数
的图象与函数 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
已知函数 是定义域为
是定义域为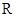 的偶函数. 当
的偶函数. 当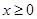 时,
时,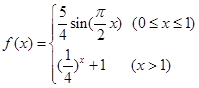 若关于
若关于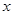 的方程
的方程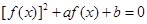 (
(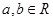 ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数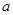 的取值范围是( )
的取值范围是( )
A.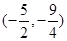 |
B.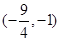 |
C.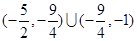 |
D.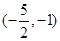 |