河北省邯郸市高三上学期1月份教学质量检测理科数学试卷
已知双曲线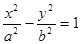 (a>0,b>0)的一条渐近线为
(a>0,b>0)的一条渐近线为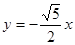 ,则它的离心率为( )
,则它的离心率为( )
A.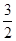 |
B. |
C.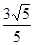 |
D.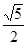 |
设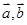 是两个非零向量,则“
是两个非零向量,则“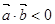 ”是“
”是“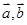 夹角为钝角”的( )
夹角为钝角”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
执行如图所示的程序框图,若输出 的值为16,那么输入的
的值为16,那么输入的 值等于( )
值等于( )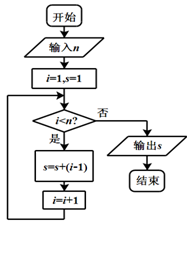
| A.5 | B.6 | C.7 | D.8 |
已知在平面直角坐标系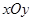 上的区域
上的区域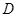 由不等式组
由不等式组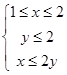 给定.若
给定.若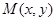 为
为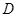 上的动点,点
上的动点,点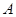 的坐标为
的坐标为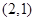 ,则
,则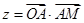 的最大值为( )
的最大值为( )
A.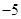 |
B.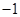 |
C.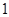 |
D. |
如图,在底面边长为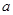 的正方形的四棱锥
的正方形的四棱锥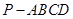 中,已知
中,已知 ,且
,且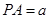 ,则直线
,则直线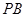 与平面
与平面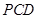 所成的角的余弦值为( )
所成的角的余弦值为( )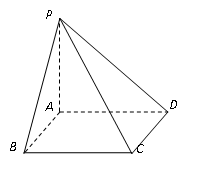
A.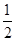 |
B. |
C.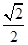 |
D.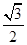 |
已知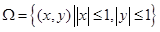 ,A是由曲线
,A是由曲线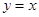 与
与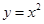 围成的封闭区域,若向
围成的封闭区域,若向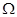 上随机投一点
上随机投一点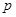 ,则点
,则点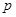 落入区域A的概率为( )
落入区域A的概率为( )
A.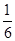 |
B.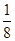 |
C.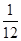 |
D.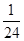 |
某几何体的三视图如图所示,则该几何体的体积为( )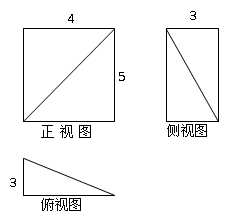
| A.10 | B.20 | C.40 | D.60 |
已知函数 是定义域为
是定义域为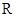 的偶函数. 当
的偶函数. 当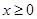 时,
时,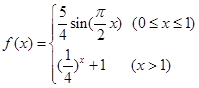 若关于
若关于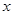 的方程
的方程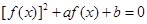 (
(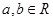 ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数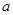 的取值范围是( )
的取值范围是( )
A.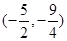 |
B.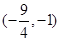 |
C.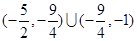 |
D.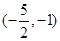 |
(本小题满分10分)等差数列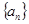 中,
中,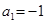 ,公差
,公差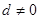 且
且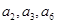 成等比数列,前
成等比数列,前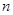 项的和为
项的和为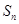 .
.
(1)求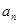 及
及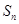 ;
;
(2)设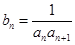 ,
,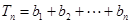 ,求
,求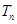 .
.
(本小题满分12分)已知
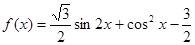
(1)求函数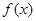 的最小正周期及在区间
的最小正周期及在区间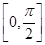 的最大值;
的最大值;
(2)在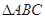 中,
中,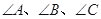 所对的边分别是
所对的边分别是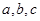 ,
,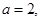
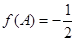 ,
,
求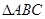 周长
周长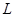 的最大值.
的最大值.
(本小题满分12分)如图,四棱锥P−ABCD中,底面ABCD为平行四边形,O为AC的中点,PO⊥平面ABCD,M 为PD的中点,∠ADC=45o,AD=AC =1,PO="a" 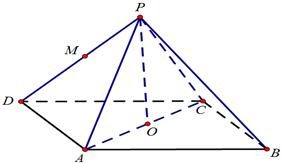
(1)证明:DA⊥平面PAC;
(2)如果二面角M−AC−D的正切值为2,求a的值.
(本小题满分12分)从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示.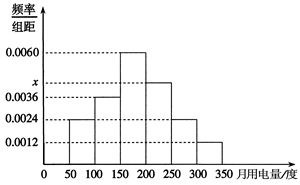
(1)根据直方图求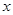 的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有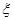 户月用电量超过300度,求
户月用电量超过300度,求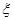 的分布列及期望.
的分布列及期望.
(本小题满分12分)已知椭圆C: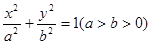 过点
过点
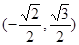 ,离心率为
,离心率为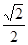 ,点
,点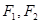 分别为其左右焦点.
分别为其左右焦点.
(1)求椭圆C的标准方程;
(2)若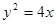 上存在两个点
上存在两个点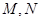 ,椭圆上有两个点
,椭圆上有两个点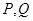 满足,
满足,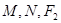 三点共线,
三点共线,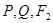 三点共线,且
三点共线,且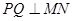 .求四边形
.求四边形 面积的最小值.
面积的最小值.
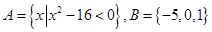 则( )
则( )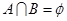

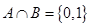
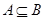
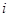 是虚数单位,则复数
是虚数单位,则复数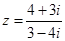 的虚部是( )
的虚部是( )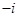
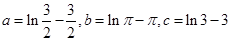 ,大小顺序正确的是( )
,大小顺序正确的是( )
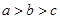
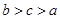

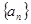 中,前10项的和等于前5项的和.若
中,前10项的和等于前5项的和.若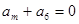 则
则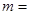 ( )
( )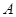 .10
.10 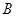 .9
.9 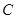 .8
.8 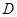 .2
.2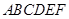 的边长为
的边长为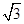 ,则
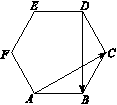
,则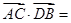 ______;
______;
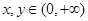 ,
,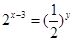 ,则
,则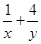 的最小值为 ;
的最小值为 ;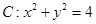 ,过点
,过点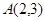 作
作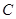 的切线,切点分别为
的切线,切点分别为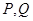 ,则直线
,则直线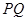 的方程为 ;
的方程为 ;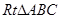 中,
中,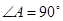 ,D是AC上一点,E是BC上一点,若
,D是AC上一点,E是BC上一点,若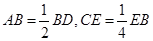 .
.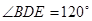 ,
,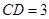 ,则BC= .
,则BC= .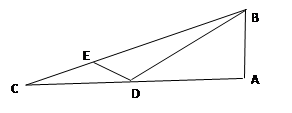
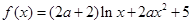
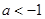 ,若对任意不相等的正数
,若对任意不相等的正数 ,恒有
,恒有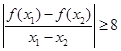 ,求a的取值范围.
,求a的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号