已知函数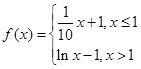 ,则方程
,则方程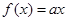 恰有两个不同实数根时,实数
恰有两个不同实数根时,实数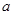 的取值范围是( )
的取值范围是( )
A.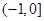 |
B.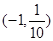 |
C.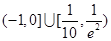 |
D.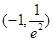 |
已知 .
.
(1)求 的单调区间;
的单调区间;
(2)令 ,则
,则 时有两个不同的根,求
时有两个不同的根,求 的取值范围;
的取值范围;
(3)存在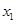 ,
,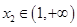 且
且 ,使
,使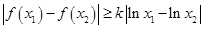 成立,求
成立,求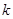 的取值范围.
的取值范围.
【原创】(本小题满分12分)已知.
(Ⅰ)求函数的最小正周期和对称中心;
(Ⅱ)将函数的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,当时,方程
的图象,当时,方程 有实数解,求实数的取值范围.
有实数解,求实数的取值范围.
已知函数 ,
, .
.
(1)若 ,判断函数
,判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若存在实数 使得关于
使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数 的取值范围.
的取值范围.
已知方程 在
在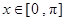 上有两个不相等的实数解,则实数
上有两个不相等的实数解,则实数 的取值范围是____________.
的取值范围是____________.
定义:对于函数 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数 ,试判断
,试判断 是否为定义域
是否为定义域 上的“局部奇函数”?若是,求出满足
上的“局部奇函数”?若是,求出满足 的
的 的值;若不是,请说明理由;
的值;若不是,请说明理由;
(2)若 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;
(3)若 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围.
的取值范围.
(本题满分14分)设 为函数
为函数 两个不同零点.
两个不同零点.
(Ⅰ)若 ,且对任意
,且对任意 ,都有
,都有 ,求
,求 ;
;
(Ⅱ)若 ,则关于
,则关于 的方程
的方程 是否存在负实根?若存在,求出该负根的取值范围,若不存在,请说明理由;
是否存在负实根?若存在,求出该负根的取值范围,若不存在,请说明理由;
(Ⅲ)若 ,
, ,且当
,且当 时,
时, 的最大值为
的最大值为 ,求
,求 的最小值.
的最小值.
已知函数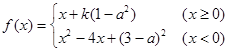 ,其中
,其中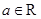 . 若对任意的非零实数
. 若对任意的非零实数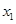 ,存在唯一的非零实数
,存在唯一的非零实数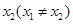 ,使得
,使得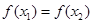 成立,则
成立,则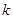 的取值范围为
的取值范围为
A.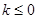 |
B.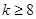 |
C.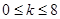 |
D.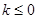 或 或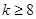 |
若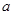 、
、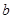 是方程
是方程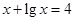 ,
,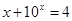 的解,函数
的解,函数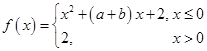 ,则关于
,则关于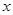 的方程
的方程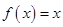 的解的个数是( )
的解的个数是( )
A.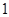 |
B. |
C.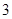 |
D.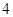 |
若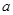 、
、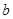 是方程
是方程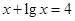 ,
,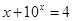 的解,函数
的解,函数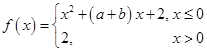 ,则关于
,则关于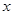 的方程
的方程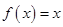 的解的个数是( )
的解的个数是( )
A. |
B. |
C.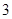 |
D.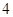 |