高中数学不定方程和方程组试题

函数f（x）=3ax﹣2a+1在[﹣1，1]上存在一个零点，则实数a的取值范围是（ ）

A．

B．a≤﹣1

C．

D．

已知函数是偶函数．
（1）求k的值；
（2）若函数y=f（x）的图象与直线没有交点，求b的取值范围．
（3）设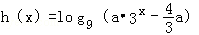，若函数f（x）与h（x）的图象有且只有一个公共点，求实数a的取值范围．

已知函数f（x）=，若存在实数a，b，c，d，满足f（a）=f（b）=f（c）=f（d），其中0＜a＜b＜c＜d，则abcd的取值范围      ．

若函数f（x）=x²+ax+1在（0，2）上有两个零点，则实数a的取值范围为     ．

函数f（x）=e^x﹣x﹣2的零点所在的区间为（ ）

A．（﹣1，0）

B．（1，2）

C．（0，1）

D．（2，3）

函数的零点有      个．

已知函数f（x）=x+2^x，g（x）=x+lnx，的零点分别为x₁，x₂，x₃，则x₁，x₂，x₃的大小关系是（ ）

A．x1＜x2＜x3

B．x2＜x1＜x3

C．x1＜x3＜x2

D．x3＜x2＜x1

已知函数f（x）=ax²+bx+c，满足f（1）=﹣，且3a＞2c＞2b．
（1）求证：a＞0时，的取值范围；
（2）证明函数f（x）在区间（0，2）内至少有一个零点；
（3）设x₁，x₂是函数f（x）的两个零点，求|x₁﹣x₂|的取值范围．

函数f（x）=2^x﹣log₂（x+4）零点的个数为      ．

设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若函数y=f（x）﹣g（x）在x∈[a，b]上有两个不同的零点，则称f（x）和g（x）在[a，b]上是“关联函数”，区间[a，b]称为“关联区间”．若f（x）=x²﹣3x+4与g（x）=2x+m在[0，3]上是“关联函数”，则m的取值范围          ．

已知函数f（x）=，若f（f（1））=4a，则实数a等于（ ）

A．

B．

C．2

D．4

下列函数中，既是奇函数又存在零点的是（ ）

A．y=cosx

B．y=sinx

C．y=lnx

D．y=

已知，则        ．

设函数，则满足的的值是（ ）

A．2

B．16

C．2或16

D．－2或16

已知函数．
（Ⅰ）求函数的极值；
（Ⅱ）设函数，若函数在上恰有两个不同的零点，求实数的取值范围．