题客网高考押题卷 第一期(新课标版)理科数学
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
| 身高x(cm) |
160 |
165 |
170 |
175 |
180 |
| 体重y(kg) |
63 |
66 |
70 |
72 |
74 |
根据上表可得回归直线方程 ,据此模型预报身高为172cm的高三男生的体重为 ( )
,据此模型预报身高为172cm的高三男生的体重为 ( )
A.70.09kg B.70.12kg C.70.55kg D.71.05kg
已知双曲线
 的左、右焦点分别为
的左、右焦点分别为 ,以
,以 为直径的圆与双曲线渐近线的一个交点为
为直径的圆与双曲线渐近线的一个交点为 ,则此双曲线的方程为( )
,则此双曲线的方程为( )
A. |
B. |
C. |
D. |
已知命题 :函数
:函数 的最小正周期为
的最小正周期为 ;命题
;命题 :若函数
:若函数 为偶函数,则
为偶函数,则 关于
关于 对称.则下列命题是真命题的是( )
对称.则下列命题是真命题的是( )
A. |
B. |
C. |
D. |
将函数 的图象向右平移
的图象向右平移 个单位长后与直线
个单位长后与直线 相交,记图象在
相交,记图象在 轴右侧的第
轴右侧的第 个交点的横坐标为
个交点的横坐标为 ,若数列
,若数列 为等差数列,则所有
为等差数列,则所有 的可能值为( )
的可能值为( )
A. |
B. |
C. 或 或 |
D. 或 或 |
已知三棱柱 的侧棱垂直于底面,各项点都在同一球面上,若该棱柱的体积为
的侧棱垂直于底面,各项点都在同一球面上,若该棱柱的体积为 ,
, ,
, ,
, ,则此球的表面积等于( )
,则此球的表面积等于( )
A. |
B. |
C. |
D. |
2014年索契冬季奥运会,已经在2014年02月07日至02月23日在俄罗斯联邦索契市举行。某校为了普及冬奥会的知识,举办知识竞赛活动.参与者需先后回答两道选择题,问题 有三个选项,问题
有三个选项,问题 有四个选项,但都只有一个选项是正确的,正确回答问题
有四个选项,但都只有一个选项是正确的,正确回答问题 可获奖金
可获奖金 元,正确回答问题
元,正确回答问题 可获奖金
可获奖金 元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
(1)如果参与者先回答问题 ,求其恰好获得奖金
,求其恰好获得奖金 元的概率;
元的概率;
(2)试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
如图所示,在四棱锥 中,底面四边形
中,底面四边形 是菱形,
是菱形, ,
, 是边长为2的等边三角形,
是边长为2的等边三角形, ,
, .
.
(1)求证: 底面
底面 ;
;
(2)求直线 与平面
与平面 所成角的大小;
所成角的大小;
(3)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ?如果存在,求
?如果存在,求 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
已知椭圆 :
: 的离心率为
的离心率为 ,直线
,直线 :
: 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆 的方程;
的方程;
(2)过 的直线
的直线 交椭圆
交椭圆 于
于 两点,则
两点,则 的内切圆的面积是否存在最大值,若存在其最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值,若存在其最大值及此时的直线方程;若不存在,请说明理由.
(本小题满分10分)选修4-1:几何证明选讲
如图, 四点在同一圆上,
四点在同一圆上, 与
与 的延长线交于点
的延长线交于点 ,点
,点 在
在 的延长线上.
的延长线上.
(1)若 ,
, ,求
,求 的值;
的值;
(2)若 ,证明:
,证明: .
.
选修4—4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆 的极坐标方程;
的极坐标方程;
(Ⅱ)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 的交点为
的交点为 ,与直
,与直
线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
 ,
, ,则图中阴影部分表示的集合为( )
,则图中阴影部分表示的集合为( )




 是纯虚数,其中
是纯虚数,其中 是实数,则
是实数,则 ( )
( )



 是
是 ,则①应为( )
,则①应为( )




 的展开式的第二项的系数为
的展开式的第二项的系数为 ,则
,则 的值为( )
的值为( )






 的焦点为
的焦点为 ,点
,点 为该抛物线上的动点,又已知点
为该抛物线上的动点,又已知点 ,则
,则 的取值范围是( )
的取值范围是( )



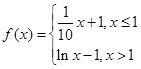 ,则方程
,则方程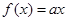 恰有两个不同实数根时,实数
恰有两个不同实数根时,实数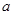 的取值范围是( )
的取值范围是( )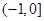
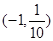
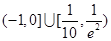
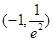
 满足
满足 ,且
,且 ,则
,则 在
在 方向上的投影为 .
方向上的投影为 . 上存在点(x,y)满足约束条件
上存在点(x,y)满足约束条件 ,则实数m的最大值为 .
,则实数m的最大值为 . 满足
满足 ,
, ,
, ,则
,则 项和
项和 = .
= . ,若对任意
,若对任意 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 . 中,
中,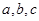 分别是内角
分别是内角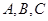 的对边,且
的对边,且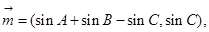
 ,且
,且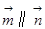 .
.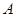 的大小;
的大小; 边上高为1,求
边上高为1,求 .
. ;
; 时,
时, ,求
,求 的取值范围.
的取值范围. ,
, .
. 的最小值;
的最小值; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号