期中备考总动员高三数学模拟卷【新课标1】3
已知复数z满足:zi=2+i(i是虚数单位),则z的虚部为( )
| A.2i | B.﹣2i | C.2 | D.﹣2 |
过抛物线y2=2px的焦点F作直线交抛物线于M,N两点,弦MN的垂直平分线交x轴于点H,若|MN|=40,则|HF|=( )
| A.14 | B.16 | C.18 | D.20 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知角 的顶点与原点重合,始边与横轴的正半轴重合,终边在直线
的顶点与原点重合,始边与横轴的正半轴重合,终边在直线 上,则cos2
上,则cos2 =
=
A.一 |
B.- |
C. |
D. |
运行如图所示的程序框图,则输出的结果S为( )

| A.2014 | B.2013 | C.1008 | D.1007 |
某工厂生产某种产品的产量x(吨)与相应的生产能耗y(吨标准煤)有如下几组样本数据:
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜率为0.7,则这组样本数据的回归直线方程是
A. =0.7x+0.35 B.
=0.7x+0.35 B. =0.7x+1
=0.7x+1
C. =0.7x+2.05 D.
=0.7x+2.05 D. =0.7x+0.45
=0.7x+0.45
【改编】已知双曲线C中心在原点,焦点 ,
, 在坐标轴上, P是双曲线上的一点,
在坐标轴上, P是双曲线上的一点, 且△
且△ 的面积
的面积 ,则双曲线C的离心率为( )
,则双曲线C的离心率为( )
A. |
B.2 | C. |
D.3 |
设函数f(x)= (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))= , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= 根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
【改编】已知A、B、C、D是球O上不同的四点,且 ,平面BCD被球所截面图形的面积为
,平面BCD被球所截面图形的面积为 ,则球O的体积为 .
,则球O的体积为 .
【原创】(本小题满分12分)△ 的内角
的内角 ,
, ,
, 所对边的长分别为
所对边的长分别为 ,
, ,
, ,向量
,向量 =
= ,
, =
= ,
, ⊥
⊥ .
.
(Ⅰ)求角B的大小;
(Ⅱ)求 的取值范围.
的取值范围.
(本小题满分12分)如图,直三棱柱 中,D、E分别是AB、
中,D、E分别是AB、 的中点.
的中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)设 ,
, ,求四棱锥
,求四棱锥 的体积.
的体积.
(本小题满分12分)某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续驶里程数R(单位:公里)分为3类,即A:80≤R<150,B:150≤R<250,C:R≥250.对这140辆车的行驶总里程进行统计,结果如下表:
(Ⅰ)从这140辆汽车中任取1辆,求该车行驶总里程超过5万公里的概率;
(Ⅱ)公司为了了解这些车的工作状况,决定抽取14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从C类车中抽取了n辆车.
(ⅰ)求n的值;
(ⅱ)如果从这n辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率.
(本小题满分12分)已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为 和
和 ,且|
,且|
 |=2,点(1,
|=2,点(1, )在该椭圆上.
)在该椭圆上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过 的直线
的直线 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A B的面积为
B的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线 相切圆的方程.
相切圆的方程.
【改编】(本小题满分12分)已知函数 .
.
(Ⅰ)设 ,若函数
,若函数 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(Ⅱ)如果当 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
如图,已知直线PA与圆O相切于点A,经过点O的割线PBC交圆O于点B和点C, 的平分线分别交AB,AC于点D和E.
的平分线分别交AB,AC于点D和E.
(Ⅰ)证明: ;
;
(Ⅱ)若 ,求
,求 的值.
的值.
以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线 的参数方程为
的参数方程为 (
( 为参数,
为参数, ),曲线
),曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线 与曲线
与曲线 相交于
相交于 、
、 两点,当
两点,当 变化时,求
变化时,求 的最小值.
的最小值.
 , 集合
, 集合 ,
,  , 则集合
, 则集合 可以表示为( )
可以表示为( )



 上单调递减的函数为( )
上单调递减的函数为( )








 的值域为( )
的值域为( )



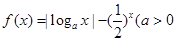 且
且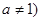 有两个零点
有两个零点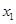 、
、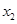 ,则有( )
,则有( )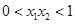
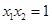
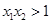
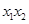 的范围不确定
的范围不确定 为单位向量,其中
为单位向量,其中 ,且
,且 在
在 上的投影为2,则
上的投影为2,则 与
与 的夹角
的夹角 ,且
,且 ,给出下列命题:
,给出下列命题: ;
; ;
; ;
; 时,
时, .
.
 的最小值为a.
的最小值为a. ,求
,求 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号