高考数学(理)一轮配套特训:2-8函数与方程
方程lnx=6-2x的根必定属于区间( )
| A.(-2,1) | B.(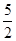 ,4) ,4) |
C.(1, ) ) |
D.( , ,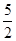 ) ) |
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
函数f(x)=(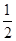 )x-sinx在区间[0,2π]上的零点个数为( )
)x-sinx在区间[0,2π]上的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
函数f(x)=ln(x+1)- 的一个零点所在的区间是( )
的一个零点所在的区间是( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
直线y=x与函数f(x)= 的图象恰有三个公共点,则实数m的取值范围是( )
的图象恰有三个公共点,则实数m的取值范围是( )
| A.[-1,2) | B.[-1,2] | C.[2,+∞) | D.(-∞,-1] |
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
函数f(x)=lnx-x-a有两个不同的零点,则实数a的取值范围是( )
| A.(-∞,-1] | B.(-∞,-1) |
| C.[-1,+∞) | D.(-1,+∞) |
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
定义在R上的函数f(x)满足f(x)+f(x+5)=16,当x∈(-1,4]时,f(x)=x2-2x,则函数f(x)在[0,2013]上的零点个数是________.
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
是否存在这样的实数a,使函数f(x)=x2+(3a-2)x+a-1在区间[-1,3]上恒有一个零点,且只有一个零点?若存在,求出a的取值范围;若不存在,说明理由.
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
已知二次函数f(x)=x2+2bx+c(b、c∈R).
(1)若f(x)≤0的解集为{x|-1≤x≤1},求实数b、c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,求实数b的取值范围.
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
已知x0是f(x)=( )x+
)x+ 的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( )
的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( )
| A.f(x1)<0,f(x2)<0 | B.f(x1)>0,f(x2)>0 |
| C.f(x1)>0,f(x2)<0 | D.f(x1)<0,f(x2)>0 |
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
已知函数f(x)= 若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
| A.(0,1) | B.(0,2) | C.(1,2) | D.(0,3) |
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
若平面直角坐标系内两点P,Q满足条件:①P,Q都在函数f(x)的图象上;②P,Q关于原点对称,则称点对(P,Q)是函数f(x)的一个“友好点对”(点对(P,Q)与点对(Q,P)为同一个“友好点对”).已知函数f(x)= ,则f(x)的“友好点对”有________个.
,则f(x)的“友好点对”有________个.
来源:2015高考数学(理)一轮配套特训:2-8函数与方程
 ,则函数f(x)的零点个数为( )
,则函数f(x)的零点个数为( ) -
- (a>0)没有零点,则实数a的取值范围为________.
(a>0)没有零点,则实数a的取值范围为________. (x>0).
(x>0). 粤公网安备 44130202000953号
粤公网安备 44130202000953号