高中数学不定方程和方程组试题

已知函数y＝f(x)和y＝g(x)在[－2,2]的图象如下图所示：

则方程f[g(x)]＝0有且仅有________个根，方程
f[f(x)]＝0有且仅有________个根．

已知函数f(x)＝x＋sin x.
(1)设P，Q是函数f(x)图像上相异的两点，证明：直线PQ的斜率大于0；
(2)求实数a的取值范围，使不等式f(x)≥axcos x在上恒成立．

已知函数f(x)＝x²－2acos kπ·ln x(k∈N^*，a∈R，且a>0)．
(1)讨论函数f(x)的单调性；
(2)若k＝2 04，关于x的方程f(x)＝2ax有唯一解，求a的值．

已知函数f(x)＝|ax－2|＋bln x(x>0，实数a，b为常数)．
(1)若a＝1，f(x)在(0，＋∞)上是单调增函数，求b的取值范围；
(2)若a≥2，b＝1，求方程f(x)＝在(0,1]上解的个数．

已知函数f(x)＝，若函数g(x)＝f(x)－k有两个不同的零点，则实数k的取值范围是________．

偶函数f(x)满足f(x－1)＝f(x＋1)，且在x∈[0,1]时，f(x)＝x，则关于x的方程f(x)＝^x在x∈[0,4]上解的个数是________．

已知函数f(x)的定义域为R，且f(x)＝，若方程f(x)＝x＋a有两个不同实根，则a的取值范围为________．

已知方程^x＝的解x₀∈，则正整数n＝________.

已知函数f（x）=x+的定义域为（0，+∞），且f（2）=2+．设点P是函数图象上的任意一点，过点P分别作直线y=x和y轴的垂线，垂足分别为M、N．
（1）求a的值．
（2）问：|PM|•|PN|是否为定值？若是，则求出该定值；若不是，请说明理由．
（3）设O为坐标原点，求四边形OMPN面积的最小值．

已知则方程所有实根的个数是（    ）

A．2

B．3

C．4

D．5

设函数 $f\left(x\right)=x^3+2a{x}^2+bx+a,g\left(x\right)=x^2-3x+2$，其中 $x\in R$， $a,b$为常数，已知曲线 $y=f\left(x\right)$与 $y=g\left(x\right)$在点 $(2,0)$处有相同的切线 $l$．
（Ⅰ）求 $a,b$的值，并写出切线 $l$的方程；
（Ⅱ）若方程 $f\left(x\right)+g\left(x\right)=mx$有三个互不相同的实根 $0,x_1,x_2$，其中 $x_1<x_2$，且对任意的 $x\in [x_1,x_2],f\left(x\right)+g\left(x\right)<m(x-1)$恒成立，求实数 $m$的取值范围．

设定义域为R的函数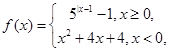若关于x的方程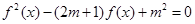有7个不同的实数解，则m=(   ).

A．2

B．4或6

C．2或6

D．6

用min{a，b)表示a，b两数中的最小值．若函数恰有三个零点，则t的值为(  )．

A．-2

B．2

C．2或-2

D．1或-l

已知函数,则下列说法错误的是(        )

A．若,则有零点

B．若有零点,则且

C．使得有唯一零点

D．若有唯一零点,则且

函数所有零点之和等于 （   ）.

A．2

B．4

C．6

D．8