已知函数,其中
,
为自然对数的底数.
(Ⅰ)设是函数
的导函数,求函数
在区间
上的最小值;
(Ⅱ)若,函数
在区间
内有零点,求
的取值范围
若函数 有极值点
有极值点 ,且
,且 ,则关于
,则关于 的方程
的方程 的不同实根的个数是( )
的不同实根的个数是( )
| A.3 | B.4 | C.5 | D.6 |
已知函数f(x)= 若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
| A.(0,1) | B.(0,2) | C.(1,2) | D.(0,3) |
已知x0是f(x)=( )x+
)x+ 的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( )
的一个零点,x1∈(-∞,x0),x2∈(x0,0),则( )
| A.f(x1)<0,f(x2)<0 | B.f(x1)>0,f(x2)>0 |
| C.f(x1)>0,f(x2)<0 | D.f(x1)<0,f(x2)>0 |
已知二次函数f(x)=x2+2bx+c(b、c∈R).
(1)若f(x)≤0的解集为{x|-1≤x≤1},求实数b、c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)内,求实数b的取值范围.
若函数f(x)=|x|+ -
- (a>0)没有零点,则实数a的取值范围为________.
(a>0)没有零点,则实数a的取值范围为________.
函数f(x)=lnx-x-a有两个不同的零点,则实数a的取值范围是( )
| A.(-∞,-1] | B.(-∞,-1) |
| C.[-1,+∞) | D.(-1,+∞) |
函数f(x)=(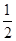 )x-sinx在区间[0,2π]上的零点个数为( )
)x-sinx在区间[0,2π]上的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
方程lnx=6-2x的根必定属于区间( )
| A.(-2,1) | B.(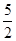 ,4) ,4) |
C.(1, ) ) |
D.( , ,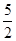 ) ) |
某小区想利用一矩形空地 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
.
(1)将五边形 的面积
的面积 表示为
表示为 的函数;
的函数;
(2)当 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.
给出定义:若m- <x≤m+
<x≤m+ (其中m为整数),则m叫做离实数x最近的整数,记作{x}=m,在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:①函数y=f(x)的定义域为R,值域为[0,
(其中m为整数),则m叫做离实数x最近的整数,记作{x}=m,在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:①函数y=f(x)的定义域为R,值域为[0, ];②函数y=f(x)在[-
];②函数y=f(x)在[- ,
, ]上是增函数;③函数y=f(x)是周期函数,最小正周期为1;④函数y=f(x)的图象关于直线x=
]上是增函数;③函数y=f(x)是周期函数,最小正周期为1;④函数y=f(x)的图象关于直线x= (k∈Z)对称.其中正确命题的序号是________.
(k∈Z)对称.其中正确命题的序号是________.