高中数学不定方程和方程组试题

若,则函数的两个零点分别位于区间（  ）

A．和内	B．和内
C．和内	D．和内

函数的零点个数为

A．1

B．2

C．3

D．4

幂函数y＝x^a，当a取不同的正数时，在区间[0,1]上它们的图象是一族美丽的曲线(如图)．设点A(1,0)，B(0,1)，连接AB，线段AB恰好被其中的两个幂函数y＝x^α，y＝x^β的图象三等分，即有|BM|＝|MN|＝|NA|.那么，αβ＝(　 　)

A．1

B．2

C．3

D．无法确定

方程的解的个数为（   ）

A．1

B．3

C．4

D．5

定义在R上的奇函数f（x），当x≥0时，，则关于x的函数F（x）=f（x）﹣a（0＜a＜1）的所有零点之和为（　　）

A．2^a﹣1

B．2^﹣a﹣1

C．1﹣2^﹣a

D．1﹣2^a

已知定义在R上的偶函数f(x)满足f(4－x)＝f(x)，且当x∈(－1，3]时，f(x)＝，则函数g(x)＝f(x)－|lgx|的零点个数是（     ）

A．7

B．8

C．9

D．10

已知是以为周期的偶函数，当时，，那么在区间内，关于的方程（且）有个不同的根，则的取值范围是（ 　）

A．

B．

C．

D．

在扶贫活动中，为了尽快脱贫（无债务）致富，企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙，并约定从该店经营的利润中，首先保证企业乙的全体职工每月最低生活费的开支3 600无后，逐步偿还转让费（不计息）．在甲提供的资料中有：①这种消费品的进价为每件14元；②该店月销量Q（百件）与销售价格P（元）的关系如图所示；③每月需要各种开支2 000元．

（1）当商品的价格为每件多少元时，月利润扣除职工最低生活费的余额最大？并求最大余额；
（2）企业乙只依靠该店，最早可望在几年后脱贫？

函数.
（1）若在其定义域内是增函数，求b的取值范围；
（2）若，若函数在 [1，3]上恰有两个不同零点，求实数的取值范围.

已知命题p：函数在上单调递减．
⑴求实数m的取值范围；
⑵命题q：方程在内有一个零点．若p或q为真，p且q为假，求实数m的取值范围．

函数在区间上的零点的个数为（   ）

A．3

B．4

C．5

D．6

对于定义域为的函数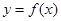，若同时满足：
①在内单调递增或单调递减；
②存在区间[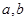]，使在上的值域为；
那么把函数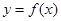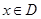（）叫做闭函数．
(1) 求闭函数符合条件②的区间；
(2) 若是闭函数，求实数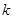的取值范围．

某小区想利用一矩形空地建市民健身广场，设计时决定保留空地边上的一水塘（如图中阴影部分），水塘可近似看作一个等腰直角三角形，其中，，且中，，经测量得到．为保证安全同时考虑美观，健身广场周围准备加设一个保护栏．设计时经过点作一直线交于，从而得到五边形的市民健身广场，设．
（1）将五边形的面积表示为的函数；
（2）当为何值时，市民健身广场的面积最大？并求出最大面积．

已知函数，那么在下列区间中含有函数零点的为(　　)

A．

B．

C．

D．

如图所示，某公园要在一块绿地的中央修建两个相同的矩形的池塘，每个面积为10000米²，池塘前方要留4米宽的走道，其余各方为2米宽的走道，问每个池塘的长宽各为多少米时占地总面积最少？