已知函数f（x）=x+2x，g（x）=x+lnx，
的零点分别为x1，x2，x3，则x1，x2，x3的大小关系是（ ）
| A．x1＜x2＜x3 | B．x2＜x1＜x3 | C．x1＜x3＜x2 | D．x3＜x2＜x1 |
已知函数f（x）=ax2+bx+c，满足f（1）=﹣
，且3a＞2c＞2b．
（1）求证：a＞0时，
的取值范围；
（2）证明函数f（x）在区间（0，2）内至少有一个零点；
（3）设x1，x2是函数f（x）的两个零点，求|x1﹣x2|的取值范围．
函数的f（x）=log3x﹣8+2x零点一定位于区间（ ）
| A．（1，2） | B．（2，3） |
| C．（3，4） | D．（5，6） |
函数f（x）=ex+x﹣2的零点所在的一个区间是（ ）
| A．（﹣2，﹣1） | B．（﹣1，0） |
| C．（0，1） | D．（1，2） |
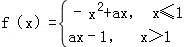若∃x1，x2∈R，x1≠x2，使得f（x1）=f（x2）成立，则实数a的取值范围是 ．
，若f（f（1））=4a，则实数a等于（ ）
，则
．
若函数
在区间
上有三个零点，则实数
的取值范围是 ．
（
为常数，
为自然对数的底数）是实数集
上的奇函数.
的方程
的根的个数.
是关于
的方程
的两根，则
的值为（ ）
，
）
）
（
为常数）是实数集
上的奇函数．
的方程
的根的个数；
．
有三个零点
、
、
，且
，则下列结论正
有两个零点，则实数b的取值范围是 ．
的零点个数是_________．
粤公网安备 44130202000953号