已知关于x的绝对值方程|x2+ax+b|=2,其中a,b∈R.
(1)当a,b满足什么条件时,方程的解集M中恰有3个元素?
(2)在条件(1)下,试求以方程解集M中的元素为边长的三角形,恰好为直角三角形的充要条件.
已知函数 ,
, ,
, .
.
(1)若 ,求证:
,求证:
(ⅰ) 在
在 的单调减区间上也单调递减;
的单调减区间上也单调递减;
(ⅱ) 在
在 上恰有两个零点;
上恰有两个零点;
(2)若 ,记
,记 的两个零点为
的两个零点为 ,求证:
,求证: .
.
已知函数 (
( ),其中
),其中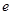 是自然对数的底数.
是自然对数的底数.
(1)当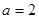 时,求
时,求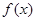 的极值;
的极值;
(2)若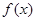 在
在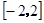 上是单调增函数,求
上是单调增函数,求 的取值范围;
的取值范围;
(3)当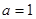 时,求整数
时,求整数 的所有值,使方程
的所有值,使方程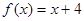 在
在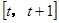 上有解.
上有解.
已知圆C过点A(1,3),B(2,2),并且直线m: 平分圆C的面积.
平分圆C的面积.
(Ⅰ)求圆C的方程;
(Ⅱ)若过点D(0,1)且斜率为k的直线 与圆C有两个不同的公共点M、N,若
与圆C有两个不同的公共点M、N,若 (O为原点),求k的值.
(O为原点),求k的值.