江苏省扬州市高三上学期期末调研考试数学试卷
某学校从高三年级共800名男生中随机抽取50名测量身高. 据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组 、第二组
、第二组 、……、第八组
、……、第八组 . 按上述分组方式得到的频率分布直方图的一部分如图所示,估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数为 .
. 按上述分组方式得到的频率分布直方图的一部分如图所示,估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数为 .

已知圆O: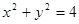 ,若不过原点O的直线
,若不过原点O的直线 与圆O交于
与圆O交于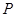 、
、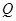 两点,且满足直线
两点,且满足直线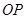 、
、 、
、 的斜率依次成等比数列,则直线
的斜率依次成等比数列,则直线 的斜率为 .
的斜率为 .
已知函数 (
( )的周期为
)的周期为 .
.
(1)当 时,求函数
时,求函数 的值域;
的值域;
(2)已知 的内角
的内角 ,
, ,
, 对应的边分别为
对应的边分别为 ,
, ,
, ,若
,若 ,且
,且 ,
, ,求
,求 的面积.
的面积.
如图,已知椭圆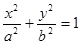 (
(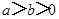 )的左、右焦点为
)的左、右焦点为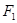 、
、 ,
,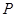 是椭圆上一点,
是椭圆上一点, 在
在 上,且满足
上,且满足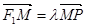 (
(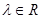 ),
),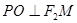 ,
, 为坐标原点.
为坐标原点.
(1)若椭圆方程为 ,且
,且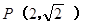 ,求点
,求点 的横坐标;
的横坐标;
(2)若 ,求椭圆离心率
,求椭圆离心率 的取值范围
的取值范围
某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系 .
.
(1)若最大拱高 为6米,则隧道设计的拱宽
为6米,则隧道设计的拱宽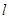 是多少?
是多少?
(2)为了使施工的土方工程量最小,需隧道口截面面积最小. 现隧道口的最大拱高 不小于6米,则应如何设计拱高
不小于6米,则应如何设计拱高 和拱宽
和拱宽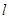 ,使得隧道口截面面积最小?(隧道口截面面积公式为
,使得隧道口截面面积最小?(隧道口截面面积公式为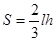 )
)
已知函数 (
( ),其中
),其中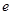 是自然对数的底数.
是自然对数的底数.
(1)当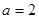 时,求
时,求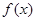 的极值;
的极值;
(2)若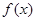 在
在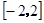 上是单调增函数,求
上是单调增函数,求 的取值范围;
的取值范围;
(3)当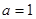 时,求整数
时,求整数 的所有值,使方程
的所有值,使方程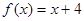 在
在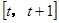 上有解.
上有解.
若数列 中不超过
中不超过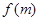 的项数恰为
的项数恰为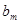 (
( ),则称数列
),则称数列 是数列
是数列 的生成数列,称相应的函数
的生成数列,称相应的函数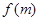 是数列
是数列 生成
生成 的控制函数.
的控制函数.
(1)已知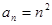 ,且
,且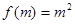 ,写出
,写出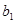 、
、 、
、 ;
;
(2)已知 ,且
,且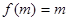 ,求
,求 的前
的前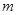 项和
项和 ;
;
(3)已知 ,且
,且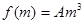 (
( ),若数列
),若数列 中,
中,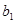 ,
, ,
, 是公差为
是公差为 (
( )的等差数列,且
)的等差数列,且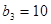 ,求
,求 的值及
的值及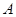 的值
的值
某商场举办“迎新年摸球”活动,主办方准备了甲、乙两个箱子,其中甲箱中有四个球,乙箱中有三个球(每个球的大小、形状完全相同),每一个箱子中只有一个红球,其余都是黑球. 若摸中甲箱中的红球,则可获奖金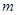 元,若摸中乙箱中的红球,则可获奖金
元,若摸中乙箱中的红球,则可获奖金 元. 活动规定:①参与者每个箱子只能摸一次,一次摸一个球;②可选择先摸甲箱,也可先摸乙箱;③如果在第一个箱子中摸到红球,则可继续在第二个箱子中摸球,否则活动终止.
元. 活动规定:①参与者每个箱子只能摸一次,一次摸一个球;②可选择先摸甲箱,也可先摸乙箱;③如果在第一个箱子中摸到红球,则可继续在第二个箱子中摸球,否则活动终止.
(1)如果参与者先在乙箱中摸球,求其恰好获得奖金 元的概率;
元的概率;
(2)若要使得该参与者获奖金额的期望值较大,请你帮他设计摸箱子的顺序,并说明理由.
 ,
, ,则
,则 .
. (
( 是虚数单位),则
是虚数单位),则 的虚部为 .
的虚部为 . 值为
值为 ,则相应输出的值为 .
,则相应输出的值为 .
 的焦点到渐近线的距离为 .
的焦点到渐近线的距离为 . 满足
满足 ,
, ,则该数列的前5项的和为 .
,则该数列的前5项的和为 . ,体积为32,则此四棱锥的侧棱长为 .
,体积为32,则此四棱锥的侧棱长为 . (
(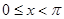 ),且
),且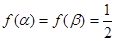 (
(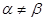 ),则
),则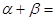 .
. ,
, ,
, ,若
,若 ,则
,则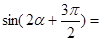 .
. 且
且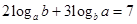 ,则
,则 的最小值为 .
的最小值为 .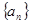 中,
中, (
( ),
),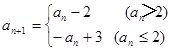 (
(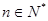 ),记
),记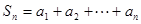 ,若
,若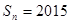 ,则
,则 .
.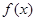 是定义在
是定义在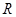 上的奇函数,当
上的奇函数,当 时,
时, . 若集合
. 若集合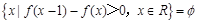 ,则实数
,则实数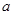 的取值范围为 .
的取值范围为 . 中,
中, ,
, 、
、 分别为
分别为 、
、 中点,
中点, .
.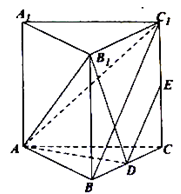
 平面
平面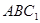 ;
;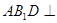 平面
平面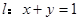 在矩阵
在矩阵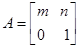 对应的变换作用下变为直线
对应的变换作用下变为直线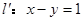 ,求矩阵
,求矩阵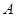 .
. 上的点到直线
上的点到直线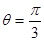 (
( )距离的最大值.
)距离的最大值. ,设数列
,设数列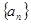 满足:
满足: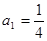 ,
,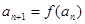 .
. ,都有
,都有 ;
;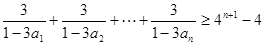
 粤公网安备 44130202000953号
粤公网安备 44130202000953号