已知圆C过点A（1,3）,B（2,2），并且直线m: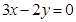
平分圆C的面积．
（Ⅰ）求圆C的方程；
（Ⅱ）若过点D（0,1）且斜率为k的直线
与圆C有两个不同的公共点M、N,若
（O为原点），求k的值．
相关试题
，
，若
，求实数a的取值范围
（
为常数），
的图象与
轴有唯一的交点，求
，
]为单调函数，求
满足
，
的解析式；相关知识点
推荐套卷
已知圆C过点A（1,3）,B（2,2），并且直线m: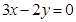平分圆C的面积．
（Ⅰ）求圆C的方程；
（Ⅱ）若过点D（0,1）且斜率为k的直线与圆C有两个不同的公共点M、N,若（O为原点），求k的值．
粤公网安备 44130202000953号