江苏省泰州市姜堰区高二下学期期中考试文科数学试卷
“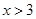 ”是“
”是“ ”的 条件. (请在“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个合适的填空
”的 条件. (请在“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个合适的填空
有下列四个命题:
①“若 ,则
,则 互为相反数”的逆命题;
互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若 ,则
,则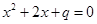 有实根”的逆命题;
有实根”的逆命题;
④“若 ,则
,则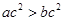 ”的逆否命题;
”的逆否命题;
其中真命题的序号为 .
设ΔABC的三边长分别为 、
、 、
、 ,ΔABC的面积为
,ΔABC的面积为 ,则ΔABC的内切圆半径为
,则ΔABC的内切圆半径为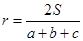 ,
,
将此结论类比到空间四面体:设四面体S—ABCD的四个面的面积分别为 ,
,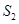 ,
, ,
,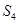 ,
,
体积为 ,则四面体的内切球半径
,则四面体的内切球半径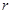 = .
= .
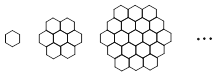
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂
巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,
以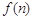 表示第
表示第 幅图的蜂巢总数,则
幅图的蜂巢总数,则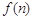 =_______.
=_______.
已知复数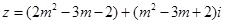 ,(其中
,(其中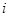 为虚数单位)
为虚数单位)
(1)当复数 是纯虚数时,求实数
是纯虚数时,求实数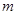 的值;
的值;
(2)若复数 对应的点在第三象限,求实数
对应的点在第三象限,求实数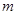 的取值范围.
的取值范围.
已知函数
(1)判定并证明函数的奇偶性;
(2)试证明 在定义域内恒成立;
在定义域内恒成立;
(3)当 时,
时,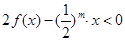 恒成立,求m的取值范围.
恒成立,求m的取值范围.
(本小题满分14分)
先解答(1),再通过结构类比解答(2):
(1)请用tanx表示 ,并写出函数
,并写出函数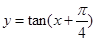 的最小正周期;
的最小正周期;
(2)设 为非零常数,且
为非零常数,且 ,试问
,试问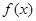 是周期函数吗?证明你的结论.
是周期函数吗?证明你的结论.
销售甲、乙两种商品所得利润分别为P(单位:万元)和Q(单位:万元),它们与投入资金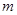 (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式 ,
,  . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资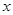 (单位:万元)
(单位:万元)
(1)试建立总利润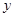 (单位:万元)关于
(单位:万元)关于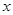 的函数关系式,并指明函数定义域;
的函数关系式,并指明函数定义域;
(2)如何投资经营甲、乙两种商品,才能使得总利润最大.
设函数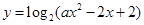 定义域为
定义域为 .
.
(1)若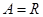 ,求实数
,求实数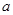 的取值范围;
的取值范围;
(2)若 在
在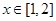 上恒成立,求实数
上恒成立,求实数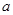 的取值范围.
的取值范围.
 ,则
,则 = .
= .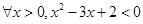 ”的否定是 .
”的否定是 . (
(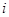 为虚数单位),则复数
为虚数单位),则复数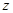 的模
的模 = .
= . 的定义域是 .
的定义域是 .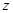 满足
满足 (
(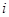 为虚数单位),则
为虚数单位),则 为 .
为 . ,若
,若 p是
p是 的取值范围为 .
的取值范围为 . ,函数
,函数 ,若
,若 ,则
,则 的值为 .
的值为 . 满足
满足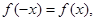 且当
且当 时总有
时总有 ,其中
,其中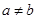 .
.  ,则实数
,则实数 的取值范围是 .
的取值范围是 .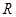 上的奇函数
上的奇函数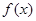 满足
满足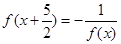 ,若
,若 ,则实数
,则实数 的取值范围为 .
的取值范围为 .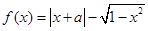 有两个零点,则实数
有两个零点,则实数 的取值范围 .
的取值范围 . 的函数
的函数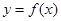 ,若同时满足:
,若同时满足: 在
在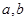 ]
] ,使
,使 上的值域为
上的值域为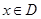 )叫做闭函数.
)叫做闭函数. 符合条件②的区间
符合条件②的区间 是闭函数,求实数
是闭函数,求实数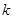 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号