高中数学不定方程和方程组试题

如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM＝PN＝MN＝2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远)．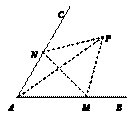

在区间上，关于的方程解的个数为         ．

已知函数，其中.
（1）若，求函数的定义域和极值；
（2）当时，试确定函数的零点个数，并证明.

某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为 $\frac{80\pi }{3}$立方米，且 $1\ge 2r$．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为 $c(c>3)$千元．设该容器的建造费用为 $y$千元．
（1）写出 $y$关于 $r$的函数表达式，并求该函数的定义域；
（2）求该容器的建造费用最小时的 $r$．

设函数中，为奇数，均为整数，且均为奇数.求证：无整数根。

设函数中，为奇数，均为整数，且均为奇数.求证：无整数根。

已知，函数的零点分别为，函数的零点分别为，则的最小值为（  ）

A．

B．2

C．

D．1

已知函数，则函数的零点个数为___________.

若等差数列和等比数列的首项均为1，且公差，公比，则集合 的元素个数最多有     个．

已知定义在实数集上的偶函数满足，且当时，，则关于的方程在上根的个数是（  ）

A．

B．

C．

D．

已知函数的零点分别为，则的大小关系是______________．

关于x的实系数方程的一个根在区间[0，1]上，另一个根在区间[1，2]上，则2a+3b的最大值为          。

平面上的点使关于t的二次方程的根都是绝对值不超过1的实数，那么这样的点的集合在平面内的区域的形状是（    ）

上海理）对区间I上有定义的函数，记，已知定义域为的函数有反函数，且，若方程有解，则

已知定义在R上的函数满足.当x［0,1］时，,若函数在区间（－1,2］有个零点，则下列命题错误的是（   ）

A．若则为1	B．若则为2
C．若，则n为3	D．n的值可能为4