山东省日照市高三5月统一质量检测考试文科数学试卷
设 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设双曲线 的离心率为
的离心率为 ,且直线
,且直线 (c是双曲线的半焦距)与抛物线
(c是双曲线的半焦距)与抛物线 的准线重合,则此双曲线的方程为( )
的准线重合,则此双曲线的方程为( )
A. |
B. |
C. |
D. |
角 顶点在坐标原点O,始边
顶点在坐标原点O,始边 轴的非负半轴重合,点P在
轴的非负半轴重合,点P在 的终边上,点
的终边上,点 ,且
,且 夹角的余弦值为( )
夹角的余弦值为( )
A. |
B. |
C. |
D. |
已知P,Q为圆 :
: 上的任意两点,且
上的任意两点,且 ,若线段PQ的中点组成的区域为M,在圆O内任取一点,则该点落在区域M内的概率为( )
,若线段PQ的中点组成的区域为M,在圆O内任取一点,则该点落在区域M内的概率为( )
A. |
B. |
C. |
D. |
三棱锥 及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为( )
及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为( )
A. |
B. |
C. |
D. |
设 是定义在R上的偶函数,且
是定义在R上的偶函数,且 时,
时, ,若在区间
,若在区间 内关于
内关于 的方程
的方程 有四个零点,则
有四个零点,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
在平面几何中有如下结论:若正三角形ABC的内切圆面积为 ,外接圆面积为
,外接圆面积为 ,则
,则 .推广到空间几何体中可以得到类似结论:若正四面体ABCD的内切球体积为
.推广到空间几何体中可以得到类似结论:若正四面体ABCD的内切球体积为 ,外接球体积为
,外接球体积为 ,则
,则 =___________.
=___________.
已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)求函数 的解析式,并写出
的解析式,并写出 的单调减区间;
的单调减区间;
(2)已知 的内角分别是A,B,C,角A为锐角,且
的内角分别是A,B,C,角A为锐角,且 的值.
的值.
某中学高三文科班学生参加了数学与地理水平测试,学校从测试合格的学生中随机抽取100人的成绩进行统计分析.抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)若在该样本中,数学成绩优秀率为30%,求a,b的值;
(2)若样本中 ,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
已知等差数列 的首项
的首项 ,公差
,公差 ,数列
,数列 是等比数列,且
是等比数列,且 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设数列 对任意正整数n,均有
对任意正整数n,均有 成立,求
成立,求 的值.
的值.
如图,在梯形ABCD中,AB//CD,AD=DC=CB=a, ,四边形ACFE是矩形,且平面
,四边形ACFE是矩形,且平面 平面ABCD,点M在线段EF上.
平面ABCD,点M在线段EF上.
(1)求证: 平面ACFE;
平面ACFE;
(2)当EM为何值时,AM//平面BDF?证明你的结论.
 等于( )
等于( )



 的实部和虚部互为相反数,那么b等于( )
的实部和虚部互为相反数,那么b等于( )



 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为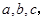 若
若 ,则角B的值为( )
,则角B的值为( )



 的部分图象大致为( )
的部分图象大致为( )
 过点
过点 ,则
,则 的最小值为_________.
的最小值为_________. ,则输出的k值为____________.
,则输出的k值为____________.
 满足约束条件
满足约束条件 的最大值为5,且k为负整数,则k=____________.
的最大值为5,且k为负整数,则k=____________. ,则函数
,则函数 的零点个数为___________.
的零点个数为___________. .
. 时,设
时,设 .讨论函数
.讨论函数 的单调性;
的单调性; .
. 过点
过点 ,且离心率
,且离心率 .
. 的直线
的直线 与该椭圆相交于A、B两点,试问:在直线
与该椭圆相交于A、B两点,试问:在直线 上是否存在点P,使得
上是否存在点P,使得 是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.
是正三角形?若存在,求出点P的坐标;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号